振動数$f$とは、1秒間あたり何回振動するか（単位:Hz = 回/s）ってこと。#波動 #共通テスト2025_第3問_問4

この問題は、グラフから振幅を読み取り、周期を求めてから振動数を計算する基本的な問題です。

解説

1. 振幅 $a_{PA}$ の読み取り

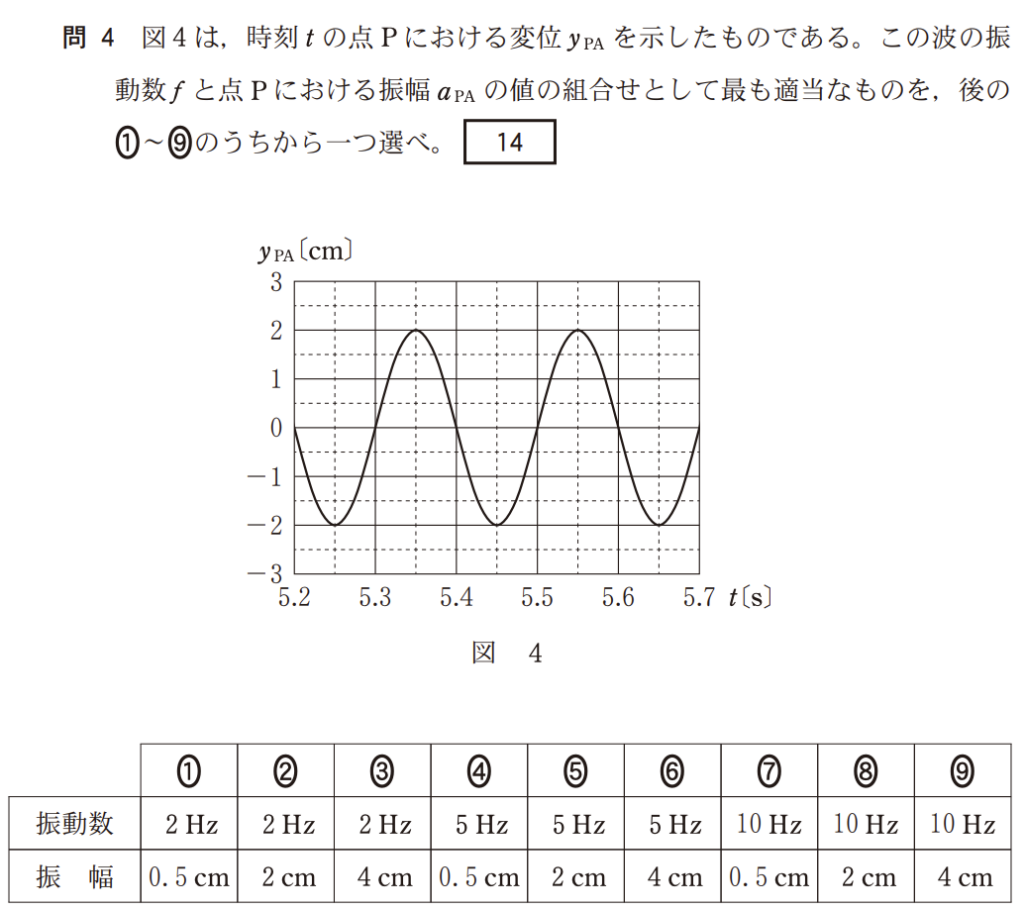
グラフの縦軸（変位 $y_{PA}$）を見ます。

波の形は、最も高いところ（山）で $+2 \text{cm}$、最も低いところ（谷）で $-2 \text{cm}$ となっています。

振幅とは、振動の中心（0）から最大変位までの大きさのことなので、

振幅 $a_{PA} = 2 \text{cm}$ です。

2. 振動数 $f$ の計算

まず、波の周期 $T$（1回の振動にかかる時間）をグラフから読み取ります。

波の形が同じ状態に戻るまでの時間間隔を探します。

• 例えば、変位が0からプラスに向かって増え始める点（立ち上がり）に注目します。

  • 1回目： $t = 5.3 \text{s}$

  • 2回目： $t = 5.5 \text{s}$

• この間隔が周期 $T$ なので、

   

  $$T = 5.5 – 5.3 = 0.2 \text{s}$$

次に、振動数 $f$（1秒間に振動する回数）を計算します。

公式 $f = \frac{1}{T}$ より、

よって、振動数 $f = 5 \text{Hz}$ です。

結論

• 振動数 $f$ ： 5 Hz

• 振幅 $a_{PA}$ ： 2 cm

この組み合わせを選択肢から探すと、⑤ が正解となります。

正解： ⑤