どうも、白滝です。
本日から、
共通テストの攻略
をお届けしていきます。
具体的には、過去問を解いていくだけですが、
解ける人間は、どういう思考で解いているのか
をマルハダカにお話しするので、、
まあまあ、タメになるはずです。w
ええ
では、始めていきましょうか。
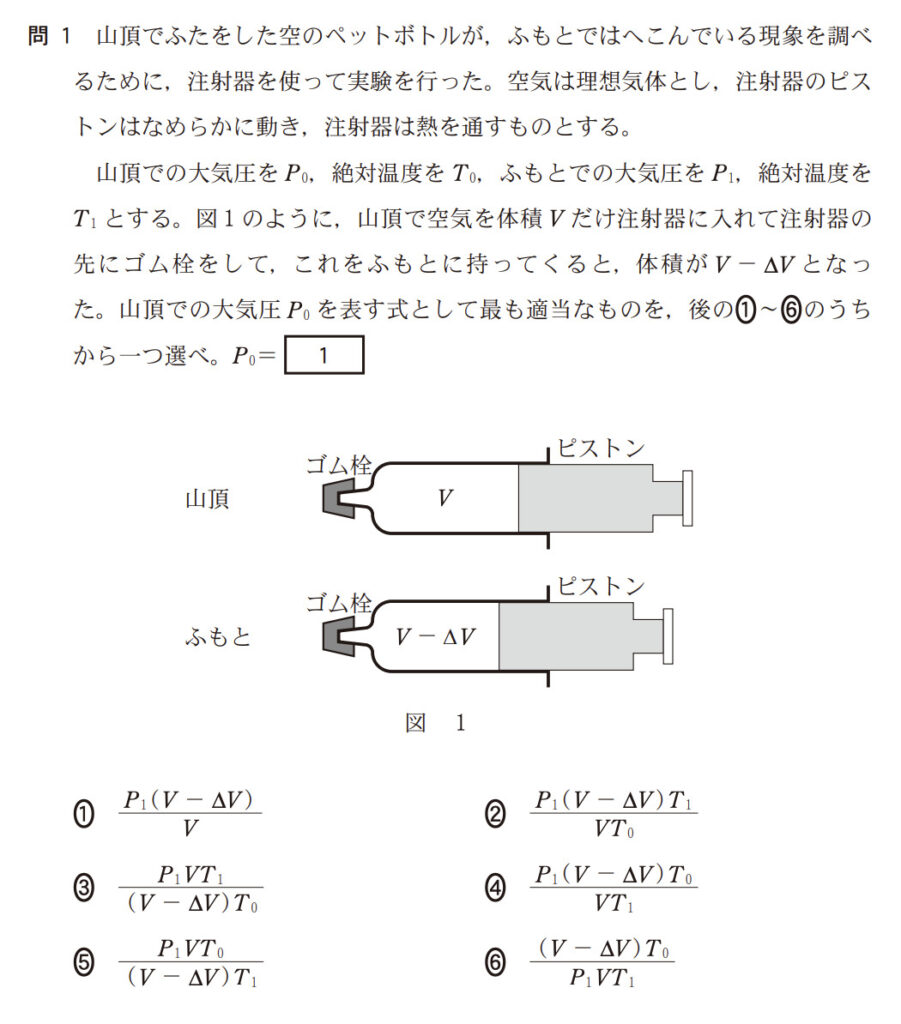
共通テスト2025_第1問_問1
(https://www.dnc.ac.jp/albums/abm.php?d=771&f=abm00005964.pdf&n=2025_op_39_butsuri.pdf)
では、思考をなぞっていきましょう。
まず、熱の問題とみた瞬間に、
PV=nRT
ΔU=W+Q
これを使って解くことが確定します。
もちろん、他のサブ公式もありますが、
主人公はこの2つだけです。
いいですか?
問題文(物理用語)を数式化する。
メルマガで散々お伝えしてきたように、
問題文(物理用語)を数式化する
のが、物理という作業です。
この問題でいえば、
- 空気は理想気体→「ああ、普通にPV=nRTを使っていいんだな」
- 注射器はなめらかに動き→「摩擦は0なんだな」→
内部と外部の空気の力の釣り合いから、「外部の気圧(大気圧)=注射器内部の気圧」 - 注射器は熱を通す→「外部の温度=注射器内部の温度」
ってことですね!
すると、問題の図に、内部の気体のパラメータが書き込めて、
山頂:$P_0$, $T_0$, $V$
ふもと:$P_1$, $T_1$, $V-ΔV$
注射器内部の物質量$n$については、
気体が漏れ出してるわけじゃない(密封状態)だから、
山頂でも、ふもとでも等しい。
よって、
山頂:$P_0$, $T_0$, $V$, $n$
ふもと:$P_1$, $T_1$, $V-ΔV$, $n$
と図に書き込めて、
あとは、山頂とふもとで、それぞれ「PV=nRT」の式を立てて(合計2本の式)、
それを計算したら完了。
答えが出てくるぜ。
物理のキモは、問題文を数式化できるか。
もっといえば、物理用語だ。
物理用語→数式
がちゃんと頭に入っているか。
変換ができるか。
ーーーー
用語を数式に翻訳する。
ーーーー
ただ、それだけ。
それだけなんだぜ。
(・・・続く)