目次
摩擦力fの向きはどっちでもいい。テキトーに置いてしまうこと。
結論から言うと、
摩擦力fの向きは、接触面の水平方向のどちらでも構いません。
もし実際は逆向きだったら、計算の結果がマイナスで出るだけですからね。
計算の結果で方向がわかるので、適当に置いちゃってください。
ルールその4.
摩擦力fの方向は、”接触面の水平方向”ならどっちに書いてもよし。
→計算の結果で「正しい」方向がわかるから。プラスなら同方向、マイナスなら逆方向。
たとえば、
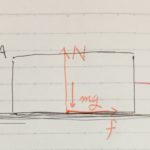
質量mの物体Aを、右向きに力Fで引っ張ったとします。
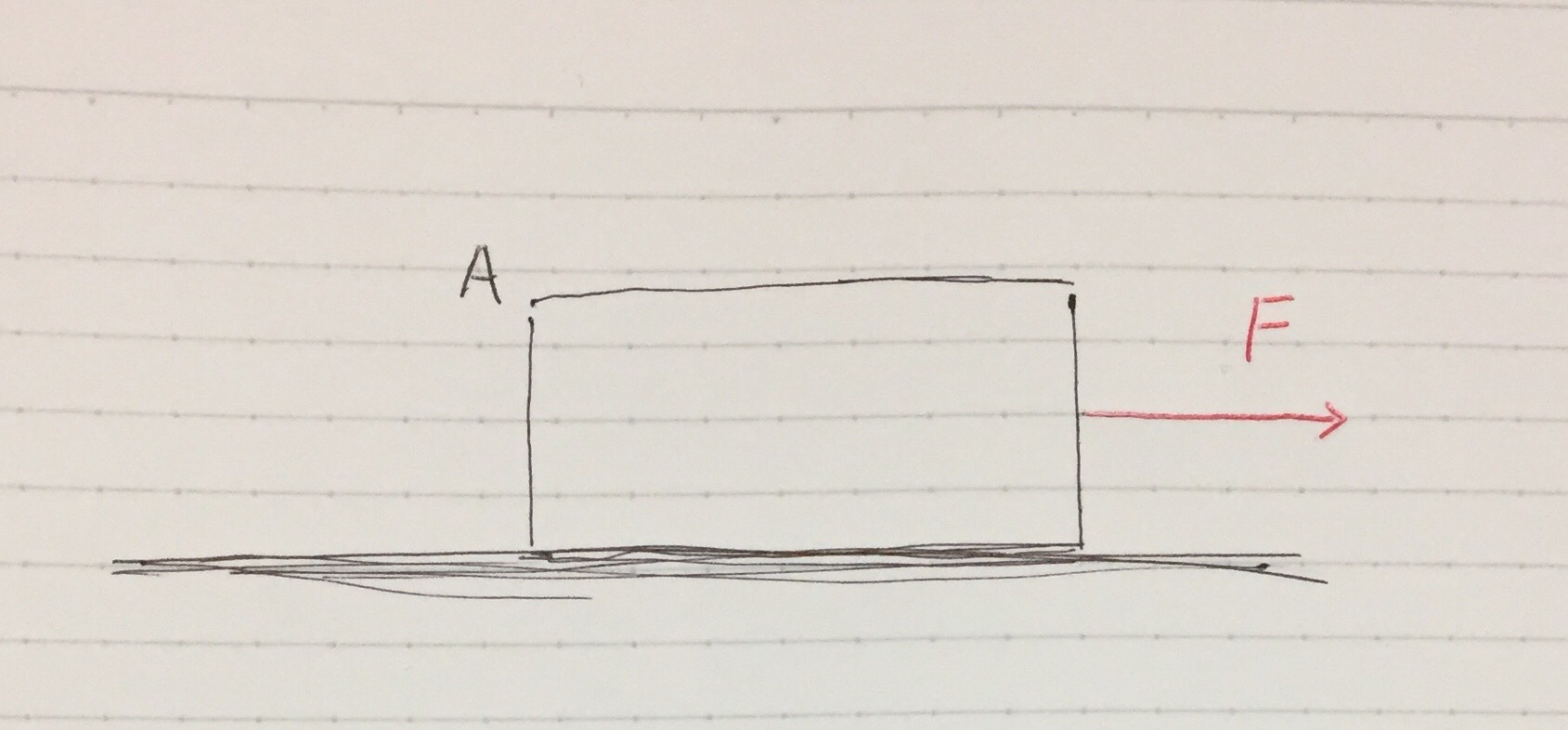
力の作図をすると、
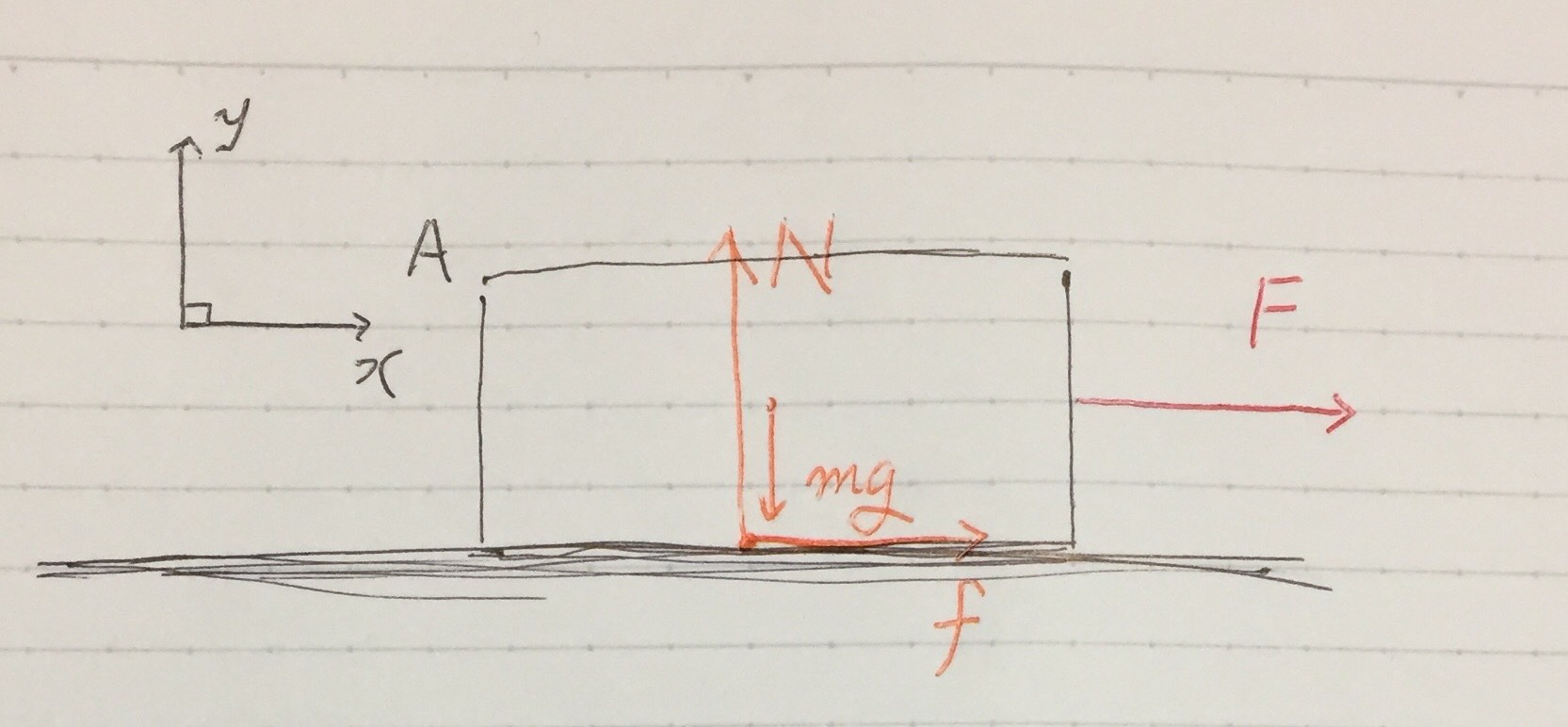
N:物体Aが床から受ける垂直抗力、mg:物体Aが地球中心から受ける引力(=重力)、f:物体Aが床から受ける摩擦力
を書き込みました。
これが、正しい「力の作図」ってやつです。
え、物体Aは右に動くはずだから、
摩擦力fの向きは左向きだって?
そんなことを
いちいち考えているから・・・
物理ができねー、ってことに
なってるんです。
物理学は「方向」も計算で導出する科目です。
多くの問題集では、「物体Aは右向きに動くから、摩擦力fを左向きにとった」とか書いてあるんですが、
これって直感の話なんですよね。
物理ですよ、「目の前の現象を数式に落とし込んで、『計算』で現象を解析する」学問ですよ。
なに勝手に、「感覚」で方向を決めてるんですか。
物理は直感も物理的センスも一切いりません。
ルール通りに力を書き込んで、ルール通りに公式に代入して、ルール通りに計算すれば、正しい答えが出るのが、物理という教科です。
物理学では、方向も計算で求めるんです。
当たり前でしょ?
「ええと、物体Aは右向きに動くから、摩擦力fは・・・」とか、直感で方向を決めるのはもうやめてください。
問題集の最初に載っているような基本問題ならともかく、
難しい問題になるほど通用しなくなってきます。
直感で摩擦力fの方向を設定して、「正解だ、よっしゃ!」とか思っているやつ、
実際の入試ではそんなカンタンな問題、出ないよ?って言いたい。
たとえば、この問題。
(外力$F_1$と$F_2$は同タイミングで発生したとし、物体Aと物体Bともに初速はゼロとする。)
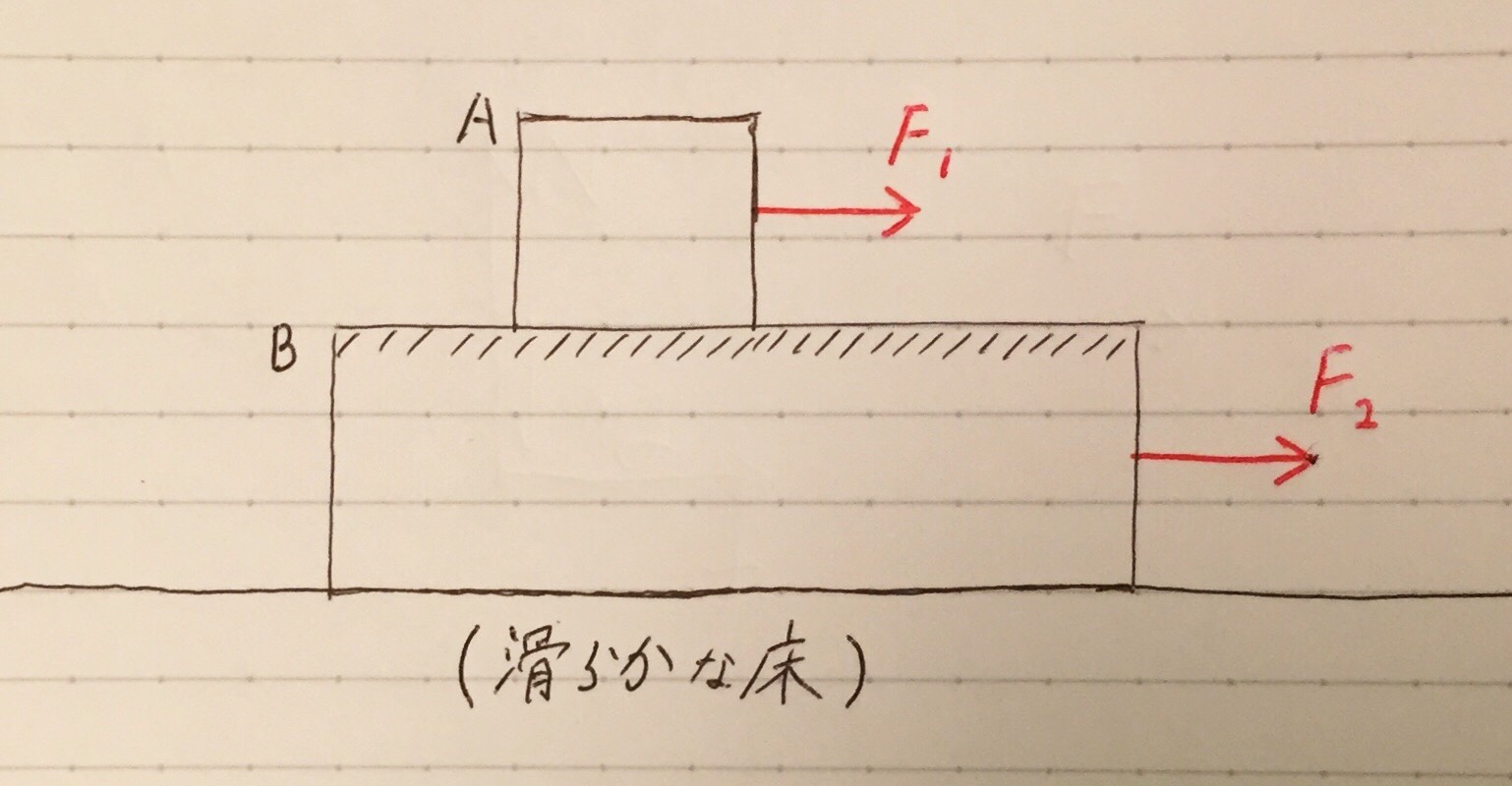
「物体Aが受ける摩擦力」を「正しい方向」に記入できますか?
ってむりでしょ。こんなの。
なぜなら、
F1とF2の大きさ次第で、摩擦力の方向が変わるからです。
でもね・・・摩擦力に向きなんて、テキトーに設定してあげればいい。
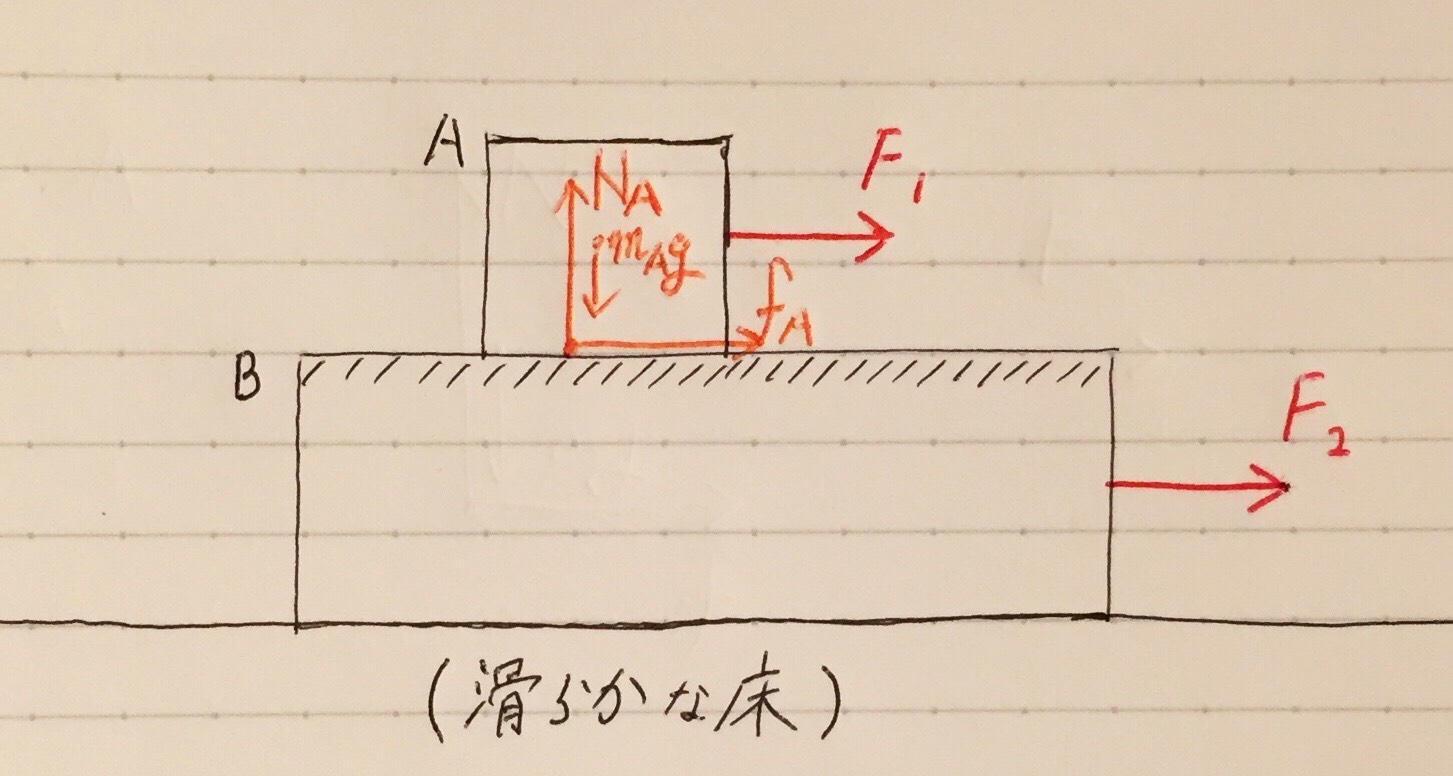
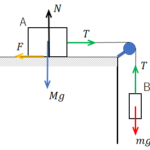
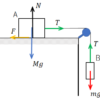
(物体Aが物体Bから受ける摩擦力:fA、物体Aが物体Bから受ける垂直抗力:NA、物体Aが地球中心から受ける引力[=重力]:mAg を記入しました。)
物体Aが受ける力は、こう記入できますね。
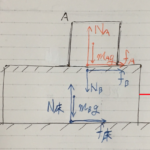
そして、物体Bが受ける力も記入してあげると、
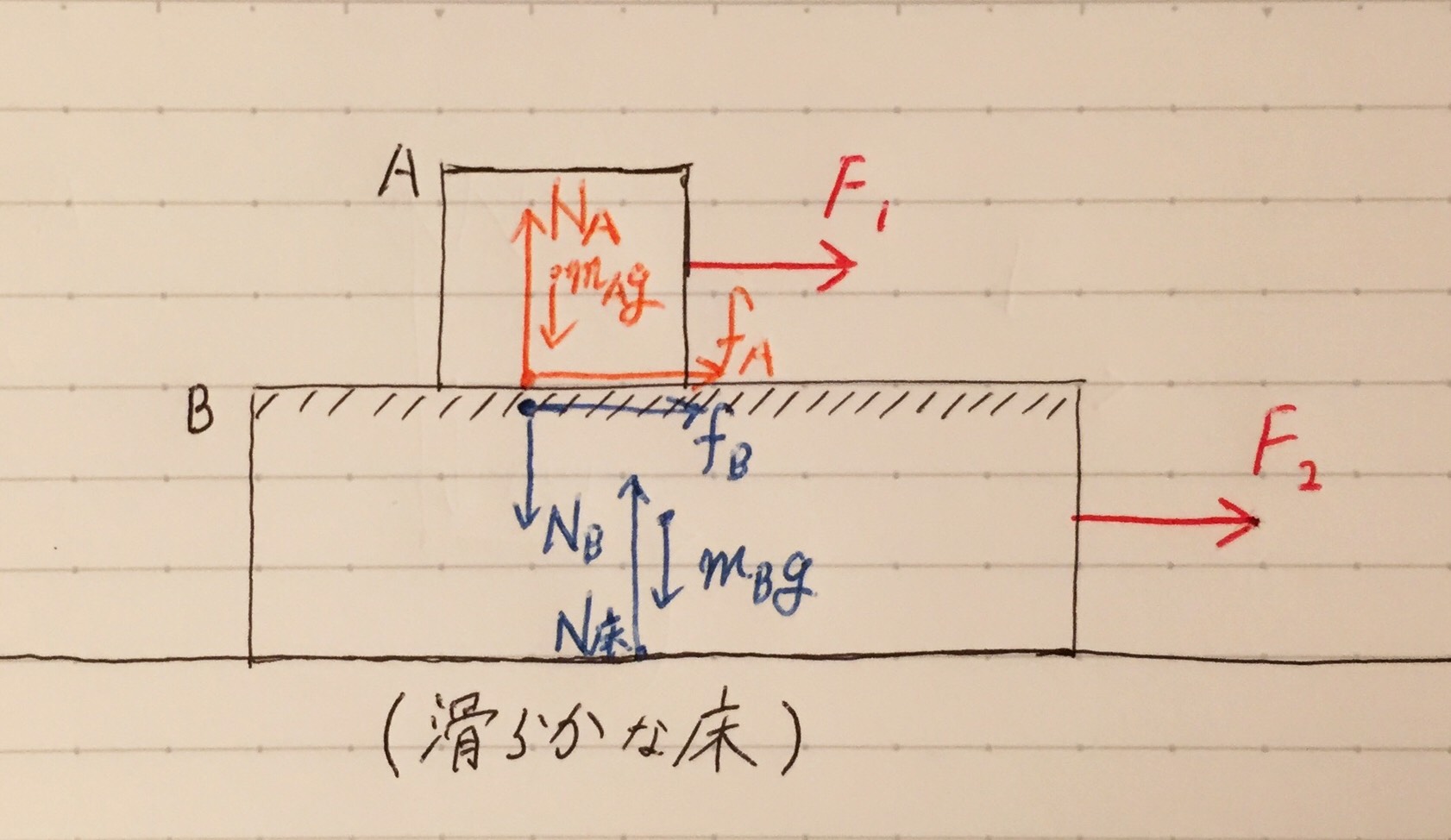
(物体Bが物体Aから受ける摩擦力:fB、物体Bが物体Aから受ける垂直抗力:NB、物体Bが地球中心から受ける引力[=重力]:mBg、物体Bが床から受ける垂直抗力:N床を記入しました。)
これで、力の作図は完成ですね。
ここから、運動方程式を立てていきます。
ルールその1.
自分でX軸とY軸を設定する。
今回は、
・右方向をX軸の正方向
・鉛直上向きをY軸の正方向
に設定してみました。
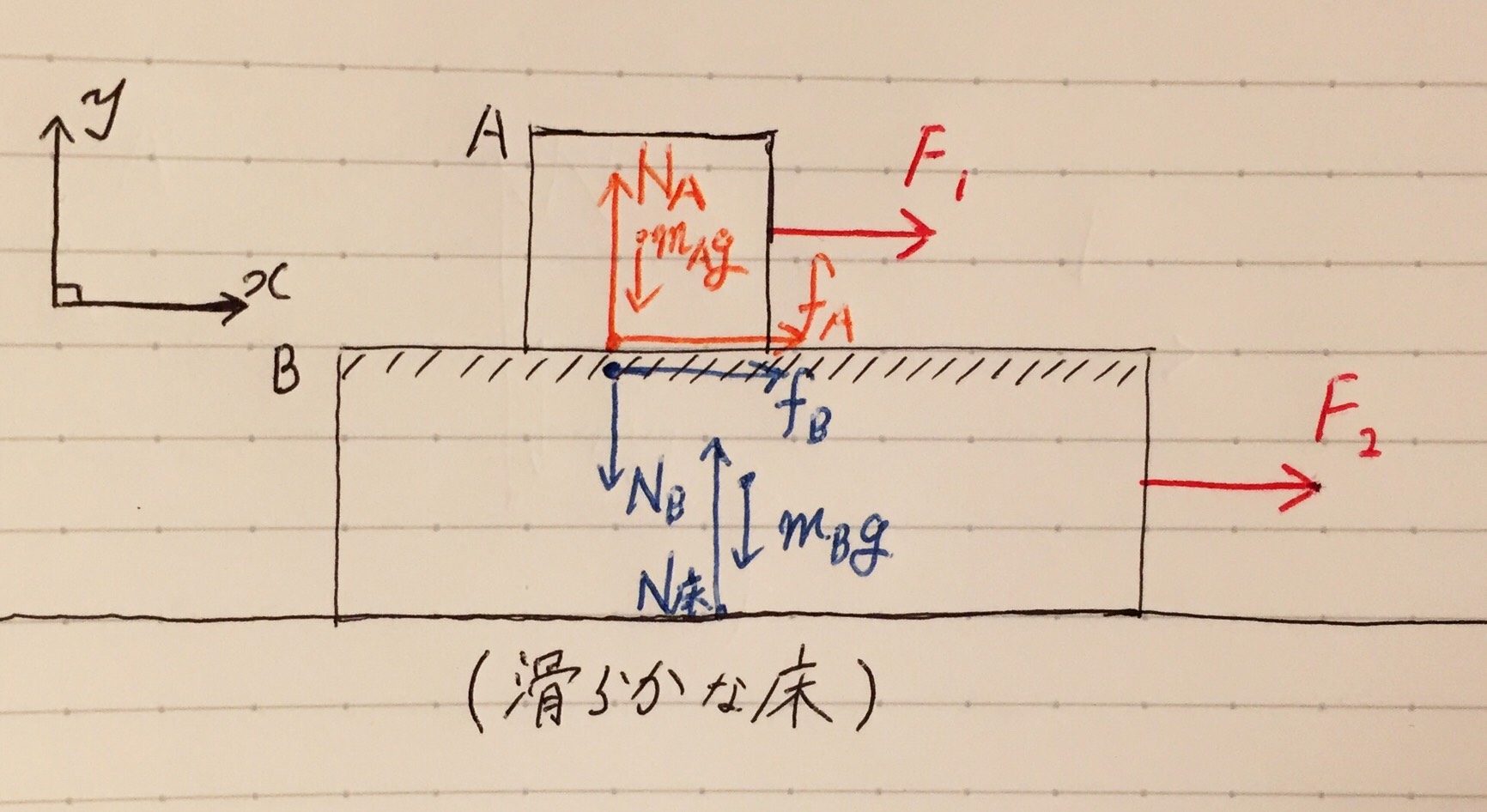
あとは、運動方程式の公式(ma=F)に代入して、式を立てるだけです。
【運動方程式】ma=F
→[質量(kg)]×[加速度(m/s²)]=[正方向にはたらく力の総和(N)]ー[負の方向にはたらく力(N)]
にそれぞれ代入するだけ。
あ、ここからはただ、「F1とF2の大きさ次第で摩擦力の方向が変わる」ことを証明するだけなので、スルーでOKです。

ふぅ・・・
こんなかんじですね。
あとは、作用反作用の法則も忘れてはいけません。

物体Aと物体B間の垂直抗力と摩擦力の「大きさ」は一致します。
(垂直抗力は最初から反対方向に設定してあるので、符号は同じですね。一方で、摩擦力は両方ともX軸の正方向に設定してあったので、計算上の符号は互いに逆の向きになります。)
これらの式を連立して、解くと、

(以下の解答を追記: 2025/12/23)
<物体Aが物体Bの上をすべっている時>
物体Aが物体Bの上をすべっているということは、
【状況1】物体Bから見て、物体Aが左にすべっている($f_A$が正)
↓
物体Bは物体Aより速い
↓
物体Bは物体Aより大きな加速度を持つ($a_A<a_B$)
【状況2】物体Bから見て、物体Aが右にすべっている($f_A$が負)
↓
物体Aは物体Bより速い
↓
物体Aは物体Bより大きな加速度を持つ($a_A>a_B$)
この2通りである。
よって、物体Aの加速度$a_A$と物体Bの加速度$a_B$の大小関係を比較すればよい。
(ここまで来れば、もう数学の問題)
(ア)より、$a_A=(F_1+f_A)/m_A$
(ウ)より、$a_B=(F_2+f_B)/m_B$
(カ)より、$f_B=-f_A$だから、
$a_A=(F_1+f_A)/m_A$・・・(ア2)
$a_B=(F_2-f_A)/m_B$・・・(ウ2)
物体Aの加速度$a_A$と物体Bの加速度$a_B$の大小関係を比較するために、
その差を$P$とすると、
$P=a_A-a_B$
(ア2)(ウ2)を代入すると、
$P=(F_1+f_A)/m_A-(F_2-f_A)/m_B$・・・(キ)
ここで上記の【状況1】【状況2】の話から、
【状況1】$f_A$が正の時、$P$は負。
$f_A>0$かつ$P<0$となる条件は、
$f_A>0$かつ、
(キ)より、$(F_1+f_A)/m_A-(F_2-f_A)/m_B>0$
$f_A>0$かつ、
$f_A<(F_1/m_A-F_2/m_B)/(m_A+m_B)$
これが成立する条件は、
$(F_1/m_A-F_2/m_B)>0$つまり、$F_1/m_A>F_2/m_B$
【状況2】$f_A$が負の時、$P$は正。
$f_A<0$かつ$P>0$となる条件は、
$f_A<0$かつ、
(キ)より、$(F_1+f_A)/m_A-(F_2-f_A)/m_B<0$
$f_A<0$かつ、
$f_A>(F_1/m_A-F_2/m_B)/(m_A+m_B)$
これが成立する条件は、
$(F_1/m_A-F_2/m_B)<0$つまり、$F_1/m_A<F_2/m_B$
よってまとめると、
$F_1/m_A>F_2/m_B$の時、$f_A$は正。
$F_1/m_A<F_2/m_B$の時、$f_A$は負。
(完了)
やはり、摩擦力fの向きは、
F1とF2の大きさによって変わることがわかりました。
あとは、摩擦力fの向きが計算の結果によってわかることも証明されましたね。
ルールその4.
摩擦力fの方向は、”接触面の水平方向”ならどっちに書いてもよし。
→計算の結果で「正しい」方向がわかるから。プラスなら同方向、マイナスなら逆方向。
摩擦力fの向きって?まとめ
摩擦力の向きは、計算の結果で判断すること。
なので、感覚で決めずにテキトーに置いちゃってください。
テキトーというのは、
一生、摩擦力を「右向き」に置いていい
ってことです。
よくわかんなかったら、
右向きに置きましょう。
計算の結果が「正」だったら右であってますし、
「負」だったら逆に左だった
と教えてくれます。
計算の結果が
ちゃんと摩擦力に向きを決めてくれますから。
以上です!
ここまでお読みいただきありがとうございました。