(https://www.u-tokyo.ac.jp/content/400239120.pdf)
そう。
やってることは物理のエッセンスと同じ。
ぱっと見はフクザツそうだけども、
実際に手を動かすと、ただのいつも通りの作業。
それが物理ですわ。w
たとえ東大でも。
京大であっても。
物理って、マジで「解き方」のパターンがないので。
少ないので。
手札をちゃんと切れば、
いつも通りに解けるのですな。
(それも、数学みたいな試行錯誤がいらない)
ね?
だから、この問題もサックリ解いてしまいましょうか。
前回の続きですね。
(前回の問題はこちら)
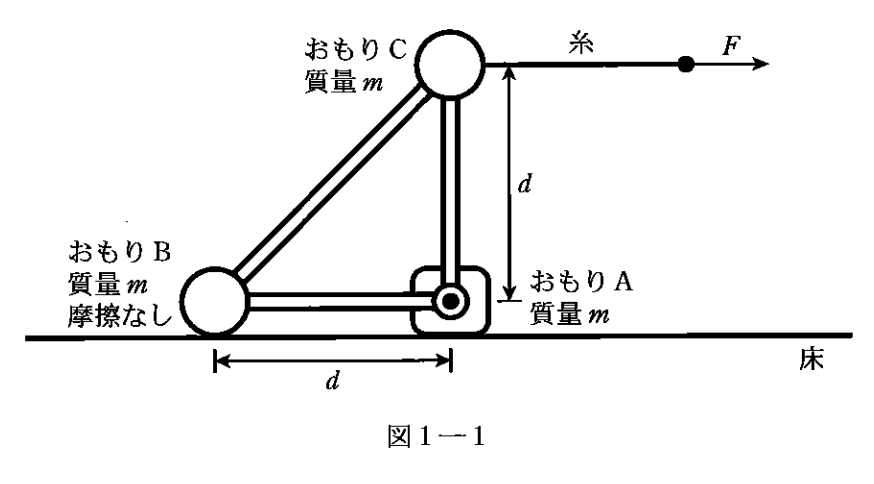
前回はこのおもりAが固定されてましたが、
今回は固定されていません。


(1)は・・・
あれ?
これは、Ⅰ-(1)で立てた式ですね。
↓
↓
例えば、(1)では、
力のつり合いか、力のモーメント
で解けばいいことがわかりますね。
おもりB, Cが動いていないことに気がついて、
力のつり合いで解くのなら、
おもりBとおもりCの両方で、
力のつり合いの式を立ててあげればいい。
間の棒は質量がゼロだから、両端にはたらく力は等しい
糸やばねと同じです。
質量がゼロなので、両端にはたらく力は等しい。
$ma=0×a=F_左-F_右$
$0=F_左-F_右$
$F_左=F_右
(糸やばねの両端の力の関係について、運動方程式を計算してみるといいぜ)
ね?
これは、質量ゼロのつなぎの棒も同じで、
両端にはたらく力は等しい。
なので、
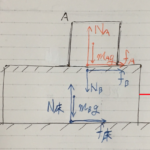
ーーーーー
棒がおもりCから受ける力をTとすると、
棒がおもりBから受ける力もTをおけるのです。
ーーーーー
これで、力Fの影響が、Tを介して伝わる。
おもりBとおもりCの両方で、
力のつり合いの式を立てて、
その式を連立して解けば、答えが出るのですな。
そう。おもりBとCの両方で、
力のつり合いの式を立ててあげればいい。
すると、
おもりBにかかる床からの垂直抗力N
が出るので・・・
それが答えですね。
Ⅰ-(1)では、このNがゼロの場合を計算したのでした。
↓
↓
もちろん、物理のエッセンスで学んだ通り、
ーーーーーー
「おもりBが床から離れた瞬間」というのは、
おもりBに対する床からの垂直抗力Nがゼロになった時
ーーーーーー
ですからね。
その瞬間($N=0$)の時のFを計算してあげればいい。
(2)も静止しているので、前問「1」と同じ条件ですね。w


なんか、おもりAが固定されていないとか言いながら、
結局、静止しとるやないかっ!!
w
という話ですが、(1)もそうですね。w
(1)だけでなく(2)も、
おもりAは実質的には固定されている。
ええ。
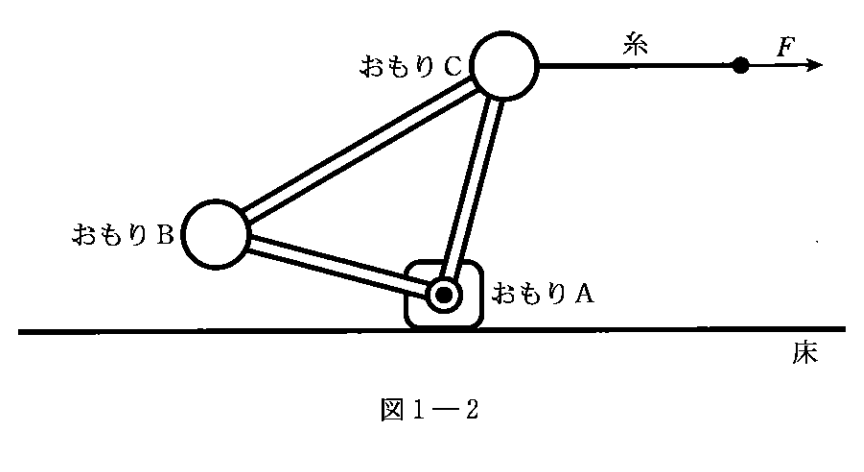
よくみると、おもりAが動くのって、(3)だけ。w
・・・・・
・・・
うわあ・・・
まあ、そんな話はさておき。
おもりAの垂直抗力はまだ求めていないので、
計算していきましょうかね。
全体から、おもりBの分を引けばいいんじゃね?

物体全体で、上下方向の力のつり合いの式を立てると、
$N_(おもりA)+N_(おもりB)=mg+mg+mg$
ここに、(1)の$N_(おもりB)$の式を使うと、
$N_(おもりA)$の式が作れるわな。
そう。
ただのつり合いの式で解けるのだ。
w
ーーーーー
静止しているから、つり合いの式が立てられる。
ーーーーー
ただ、それだけです。
(3)でやっと、おもりAが動き出す。
とは言っても・・・
ねえw
ただの「静止摩擦力の大きさ」を求める問題ですねw
(求めて、$F=・・・$の形に変形すればよい)


全体をみると、横方向の力のつり合いは
$(おもりAの摩擦力)=F$
ですね。
んで、
ご存知かと思いますが、
最大静止摩擦力(滑らない状態での最大のまさつ力)を求める公式は、
最大静止摩擦力=(静止摩擦係数)×(垂直抗力)
ですから・・・
この通りに求めればよし。
具体的には、
おもりAの垂直抗力: (2)で求めた$N_(おもりA)$
静止摩擦係数: 問題文にある$μ$
これをかけるだけで、
おもりAの最大静止摩擦力が出ますね。w
すると、先ほどのつり合いの式から、
$N_(おもりA)×μ=F$
となるから、
あとはこれを$F$について解くだけ。
算数の話です。
ええ。
では、今日はここまで。
また次の問題でお会いしましょう。