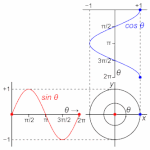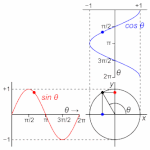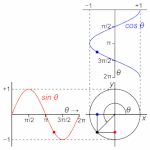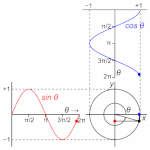
位相とは、なにか?
周期とは、円である。
そう定義した瞬間から、
周期的な運動が、
数式で表せるようになった。
すると、
計算が
できるようになったんだな。
ミライの
物体の加速度を。
ミライの
物理現象の様子を。
計算できる。
シミュレーションできる。
周期的な運動が、
予測できるようになったのだ。
そのための定義。
周期とは、円である。
位相とは、
そこで登場した、
周期の「途中の状態」のことを
いうのである。
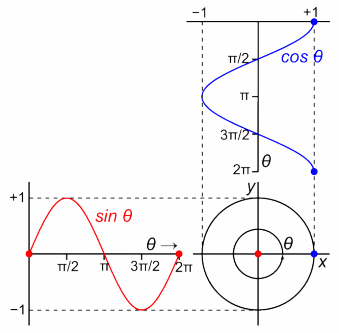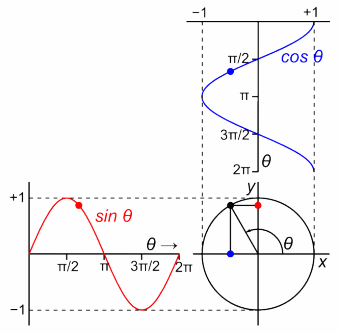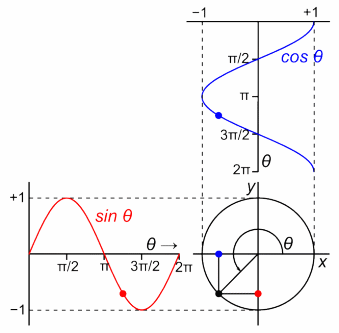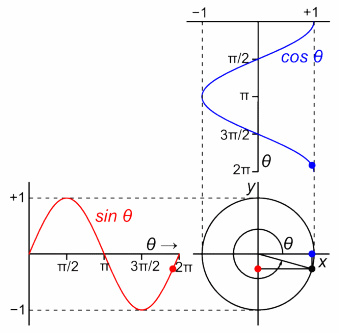
1周期は円1周。
当時の物理学者は、
繰り返しの様子を、
円1周
で表そうと考えた。
1周期は円1周。
つまり、
1周期=角度2π回転すること
って考えたのだ。
そう定義すると、
円周をグルグル回る様子と、
周期的な運動が
1対1で対応することに
気づいたから。
円は繰り返し。
円は昔から、
無限の象徴でしたから。
数学的にも、
円は、
2πで同じ位置に
戻ってきますからね。
(2πごとに、同じ運動を繰り返す。)
だから、、
物理や数学では(学問の分野では)、1周期を角度2πでわけて、円の1周で1周期を表すことにしました。
1周期は円1周。
1周期は
角度2πを回転すること。
そう定義した。
すると、
角度θが、周期の途中段階を表すことに気付きました。
1周期、2周期目、3周期目・・・
と数えるだけじゃなくて、
1周期と角度πのところ、
2周期と角度π/4のところ・・・
と示せることに気づいた。
周期の途中。
それを、
数字で示せることに気づいた
んです。
円を1周するまで、角度が2πに達するまでの途中の段階。
それが、位相です。
位相は、
2πで1周期と定義したときの、
周回の余り。
〇周期とするには
余分な角度θ(シータ)。
これが、
位相を表す値となる。
0≦θ<2π
という
但し書きがつくけどね。
2πで1周期だから、
角度が3πだったら、1周期分の2πを取り除いて、
πが位相。
(周回できなかった余り分)
位相とは、
周期の途中の状態
のことだから。
1周期まわって、2周期まわって、、
その間の一瞬。
周期の途中。
それがどんな状態にあるのか・・・
が位相。
周期の途中の状態は、
「位相」が示してくれる。
だって、
位相は周回の余りだからね。
位相とは、周期の「途中の角度」をいう。
お忘れなきように。