
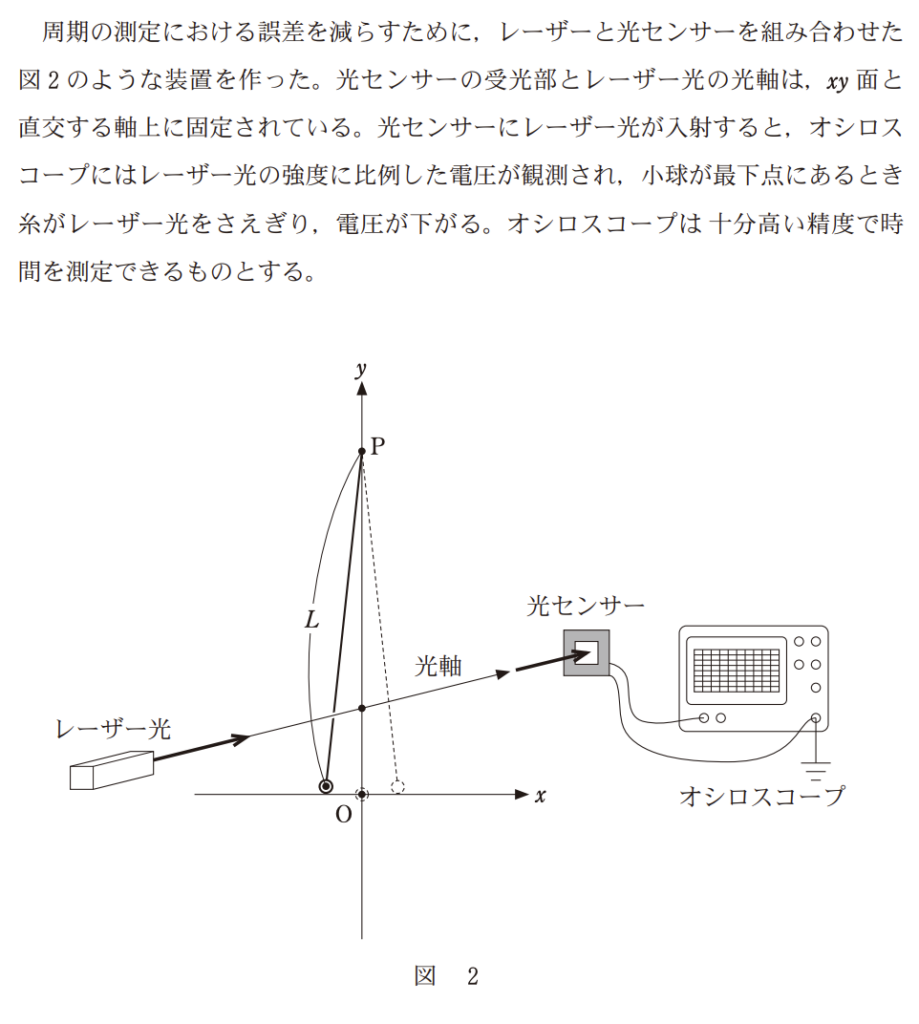
(https://www.dnc.ac.jp/albums/abm.php?d=771&f=abm00005964.pdf&n=2025_op_39_butsuri.pdf)
まるで、小学校の文章問題。w
知識ではなく、
問題文から数式を立てて、その意味を読めるか?
が問われてますね。
ええ。
焦らずに。
正しく式を立てて、
それを正しく読みましょう。
意味を取りましょう。
ただ、それだけの問題ですぜ。
(以下、Gemini3の解答)
解説
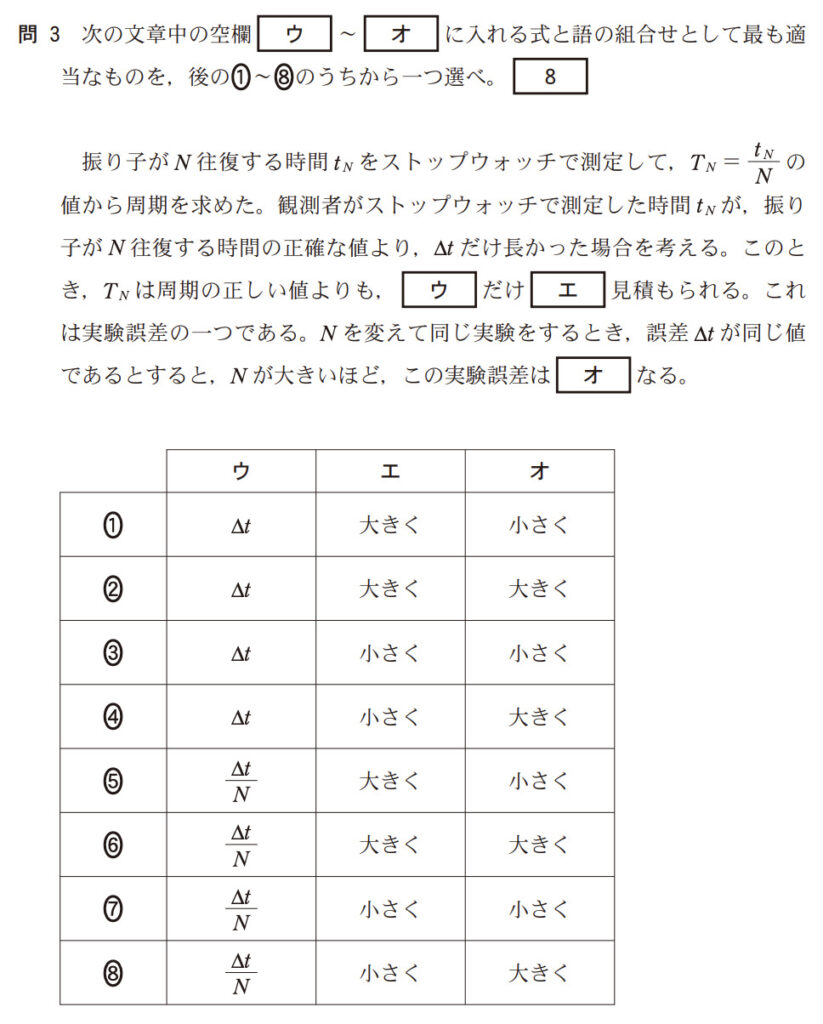
1. 空欄 [ウ]:周期のずれの大きさ
本来の正しい $N$ 往復の時間を $t$ とします。
観測者が測定した時間 $t_N$ は、正しい時間より $\Delta t$ だけ長かったので、
と表せます。
このとき、求められる周期 $T_N$ は以下のようになります。
本来の正しい周期は $T = \frac{t}{N}$ です。
よって、測定値 $T_N$ と真の値 $T$ の差(ずれ)は $\frac{\Delta t}{N}$ となります。
2. 空欄 [エ]:ずれの方向
測定した時間 $t_N$ が「長かった」のですから、割り算して求めた周期 $T_N$ も当然、本来の値より 大きく 見積もられます。
(式を見ても、$T_N = T + \frac{\Delta t}{N}$ とプラスされていることからも分かります)
3. 空欄 [オ]:$N$ を大きくした時の誤差
実験誤差(周期のずれ)は $\frac{\Delta t}{N}$ で表されます。
ここで、誤差 $\Delta t$(ストップウォッチを押すタイミングのずれなど)が毎回一定であると仮定しています。
分母の $N$(往復回数)を大きくすると、分数全体の値 $\frac{\Delta t}{N}$ は小さく なります。
つまり、たくさん往復させてから時間を測って平均をとるほど、1回あたりの周期に含まれる誤差は薄まって小さくなるということです。
結論
-
[ウ]: $\frac{\Delta t}{N}$
-
[エ]: 大きく
-
[オ]: 小さく
この組み合わせを選択肢から探すと、⑤ が正解となります。
正解: ⑤







