
(https://www.dnc.ac.jp/albums/abm.php?d=771&f=abm00005964.pdf&n=2025_op_39_butsuri.pdf)
どうも、白滝です。
- 波源Aから出た波の点Pにおける変位
- 波源Bから出た波の点Pにおける変位
- その合成波(点Pにおける)
のうち、aとcがあって、
そこからbを推測すればよい。
aとbを足したら、cになるわけだから、
例えば$t=5.35[s]$で$-1.5[cm]$となるbを選べばよい。
(これで、②しかないことがわかる)
======
波の全体を見ていると、ちょっとわかりにくいが、
具体的な1点の足し算・引き算を考えると解きやすいぜ!
======
ーーーーーーー
いろいろ書いてあるが、
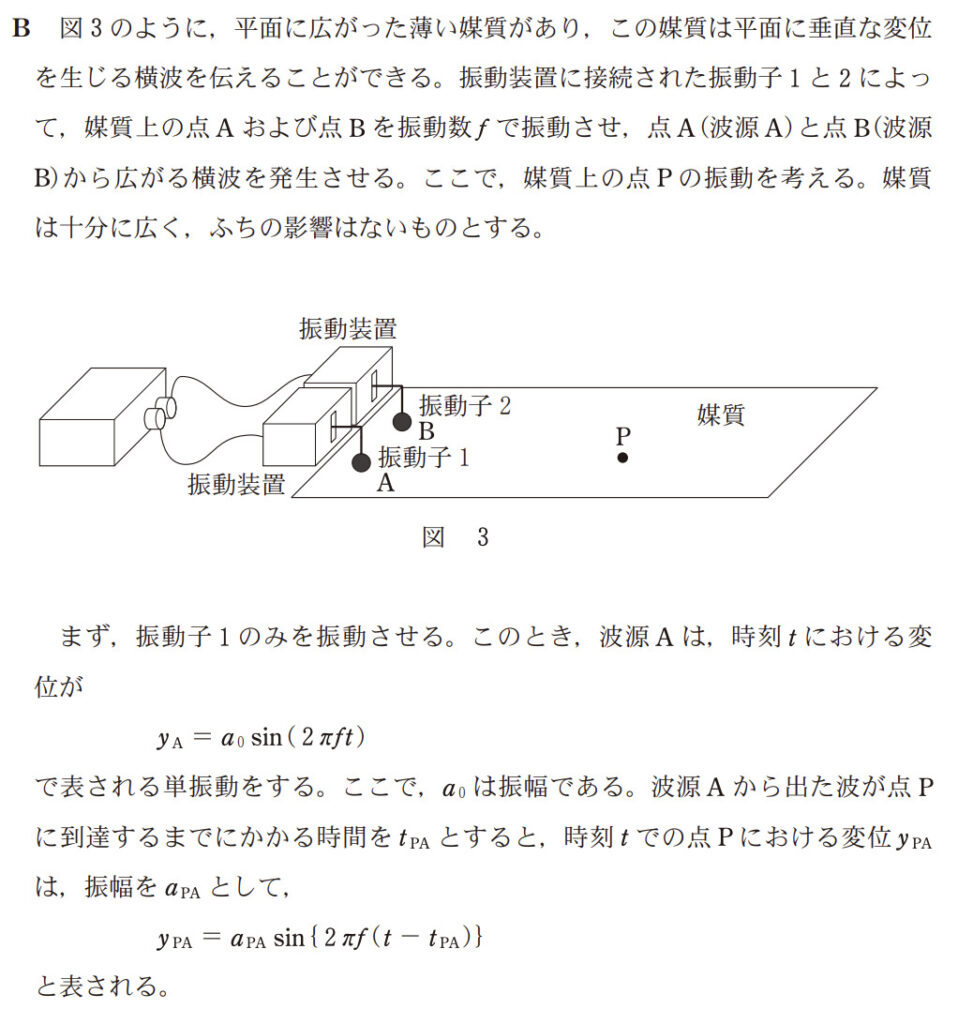
「波源から出た波」「点Pに届くまでの時間」は考えなくてよい。
結局のところ、「点Pにおける変位」だけを考えればよい
(と問題文から読み取りたい)問題でっせ。
ーーーーーーー
↓
↓
(Gemini3の解答)
この問題は、**「波の重ね合わせの原理($y_P = y_{PA} + y_{PB}$)」**を利用して、結果の波形と一方の波形から、もう一方の波形を逆算する問題です。
解説
1. 関係式の整理
振動子1と振動子2を同時に動かしたときの変位 $y_P$ は、それぞれの波の変位 $y_{PA}$ と $y_{PB}$ の和になります。
求めたいのは振動子2による波 $y_{PB}$ なので、式を変形します。
つまり、「合成波のグラフ(図5)」から「振動子1のグラフ(図4)」を引き算すれば、答えのグラフが求まります。
2. 具体的な時刻での値を読み取る
グラフの特徴的な点(山や谷)に注目して計算します。
-
時刻 $t = 5.25\text{s}$ のとき(5.2と5.3の真ん中):
-
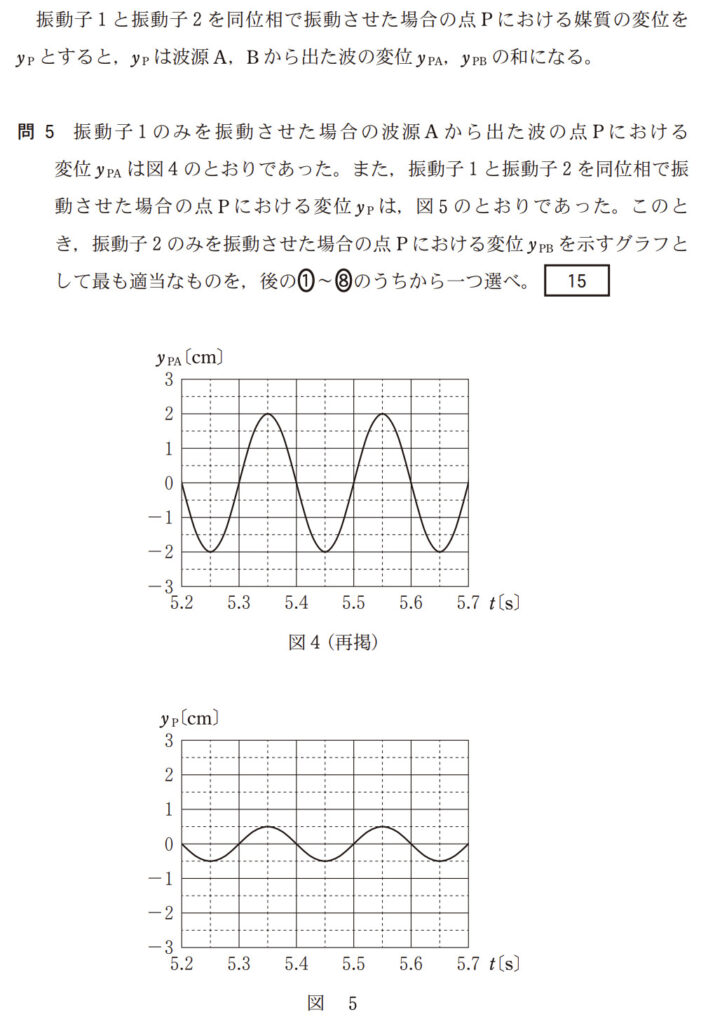
図4 ($y_{PA}$): 谷の底になっています。値は $-2.0 \text{cm}$ です。
-
図5 ($y_P$): 同じく谷の底ですが、浅くなっています。値は $-0.5 \text{cm}$ です。
-
計算 ($y_{PB}$):
$$y_{PB} = (-0.5) – (-2.0) = \mathbf{+1.5 \text{cm}}$$ -
つまり、この時刻で $+1.5 \text{cm}$(山) となるグラフを探せばよいことになります。
-
-
時刻 $t = 5.35\text{s}$ のとき(5.3と5.4の真ん中):
-
図4 ($y_{PA}$): 山の頂上です。値は $+2.0 \text{cm}$ です。
-
図5 ($y_P$): 同じく山の頂上です。値は $+0.5 \text{cm}$ です。
-
計算 ($y_{PB}$):
$$y_{PB} = (+0.5) – (+2.0) = \mathbf{-1.5 \text{cm}}$$ -
つまり、この時刻で $-1.5 \text{cm}$(谷) となります。
-
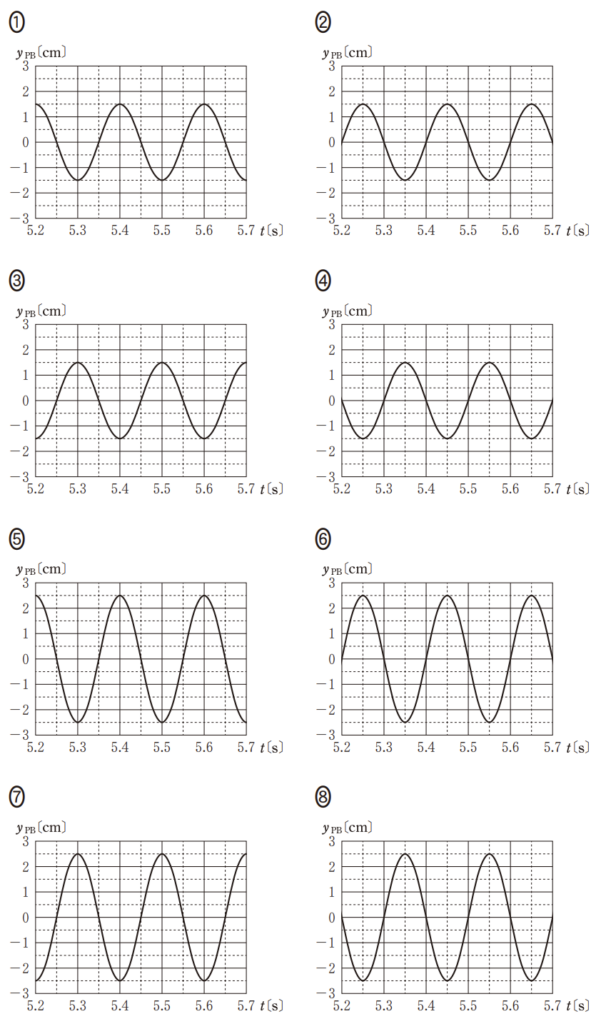
3. 選択肢の検討
上記の条件(振幅が $1.5 \text{cm}$ で、最初の山が先に来る)を満たすグラフを探します。
-
振幅の確認:
計算結果より、振幅は $1.5 \text{cm}$ です。
振幅が $2.5 \text{cm}$ になっている⑤~⑧は除外されます。①~④が候補です。
-
位相(波の形)の確認:
$t = 5.25\text{s}$ で $+1.5 \text{cm}$(正の値) になっているものを選びます。
-
①:$t=5.2$ で既に $+1.5$ から始まっている(cos型)。×
-
②:$t=5.2$ から上がり始め、$t=5.25$ で $+1.5$ になる。〇(正解)
-
③:$t=5.2$ で $-1.5$ から始まっている。×
-
④:$t=5.2$ から下がり始め、$t=5.25$ で $-1.5$ になる(逆位相)。×
-
結論
時刻 $5.25\text{s}$ 付近で山(正の変位)となり、振幅が $1.5\text{cm}$ であるグラフは ② です。
正解: ②