どうも、白滝です。
位相は英語で言うと
phase(フェイズ)
ですよね。
フェイズ。
なんか、聞いたことありません?
そう。

遊戯王ですよね。
遊戯王のデュエルで使われる、用語たち。
ドローフェイズ、メインフェイズ、バトルフェイズ・・・を経て、ターンエンド。
これが、位相の基本。
位相ってやつの
本質を表しているんですわ。
たとえば、遊戯王では、「俺のターン」を周期的に繰り返してバトルをする。
1ターンが1周期。
その1ターンに含まれる各場面を、
フェイズ(位相)と呼んだ。
(ドローフェイズ、メインフェイズ、バトルフェイズ・・・を経て、ターンエンド。これが1周期。)
1周期が終わるまでの、各段階。
それが位相ってこと。
1ターンが終わるまでの各段階。
それがフェイズってこと。
位相(phase)ってのは、
周期的に変わるホニャララの、その周期状態を表すものなのだ。
うーん?
わかりづらい?
そもそも、周期的ってなに?「周期」ってなんで必要なの?
と思いますよね。
この世には、
周期性のある運動がたくさんある。
円の回転も。
バネの振動も。
水の振動も。
同じ様子が、
ひたすら繰り返される運動なのだ。
それが、周期的ってこと。
同じ模様が繰り返される。
同じ動きが繰り返される。
そんでね、
物理学者は考えたのだ。
それを、どうしても数式で表したい。
周期性のあるものを、
どうしても数学の世界に
落とし込みたかった。
だから、、
物理や数学の世界では(学問の分野では)、その周期を角度2πでわけて「円の1周で1周期を表す」と定義しました。
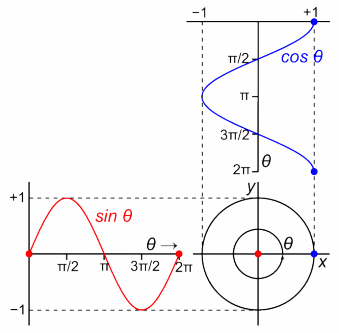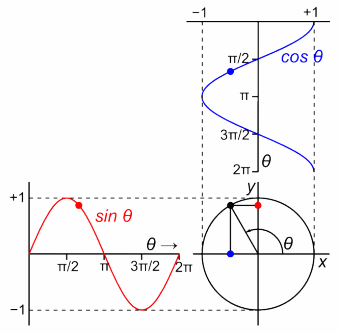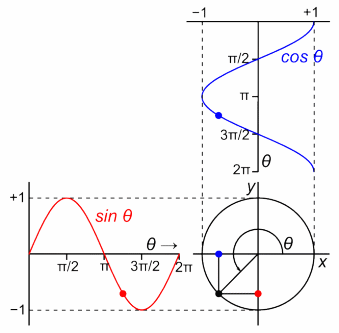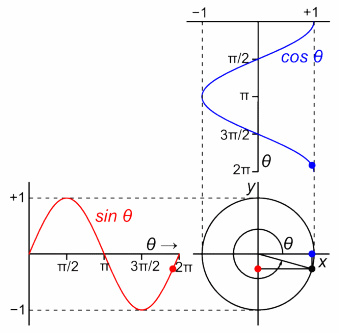
そうすれば、
計算ができるからね。
周期性のある運動を、
計算で予測することができる。
だから、
学者は等速円運動で「周期」を定義
することにしたんです。
周期性のある運動の中で、
1番単純だから。
周期を円を使って考えた。
1周期を角度2πでわけて、円の1周で1周期を表す
とした。
等速円運動。
単位円。
三角関数は、
その計算ツール。
円1周分の角度で、1周期。
2πで1周期と定義して、、
たとえばね、
固定端反射では、
その周期が+π進むって発見した。
固定端反射した時、
その振動は
1周期の半分だけ進んだものに
変わるってことね。
こうやって、
1周期を2πという角度でわけたことで、
1周期の途中のところを、数字で示せるようになったんだ。
半周期をπと書けた。
4分の1周期をπ/2と書けた。
つまり、
1周期の途中を
数字で扱えるようになったわけだ。
そして、
この数字を「位相」という。
1周期の途中。
その段階。
それが、位相(phase)。
ドローフェイズ、メインフェイズ、バトルフェイズ・・・を経て、ターンエンド。
遊戯王の1ターンと同じですね。
各段階に名前をつけることで、
1周期の中でも「わけて」扱うことができた。
物理や数学でも、
1周期は円の1周(2π)
と定義したことで、
1周期の途中を
「角度」で示すことができた。
位相とは、
1周期の途中を示す角度のこと。
0≦θ<2π
の角度のことをいうのです。