「慣性力」を１００％確実に解く方法。（再掲）

 

慣性力を、もっとロジカルに。

 

私も高校生時代は、

慣性力というものがわかりませんでした。

 

 

まとめるとこんなもんですが、

これめっちゃイメージで説明されません！？

 

電車の中で、つり革が動くから・・・とか、

バスに乗っていて急加速するとバランスを崩す・・・とか。

 

意味わからん。w

 

ロジカルなのが、物理なのに。

 

ネットで調べても、

こんな解説ばかり載っていますよね？

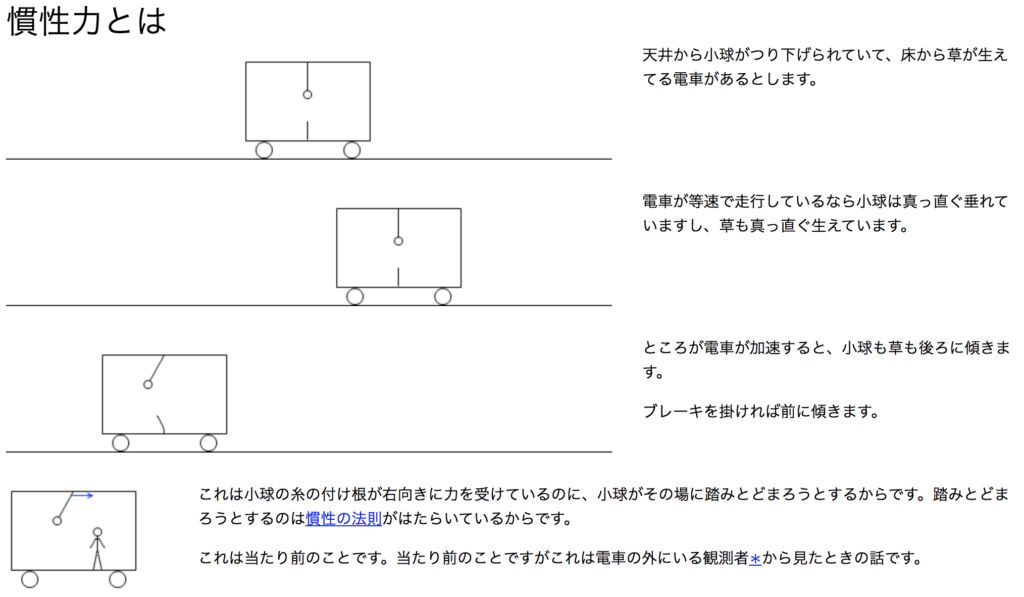
（わかりやすい高校物理の部屋『慣性力』より引用）

 

で？

 

っていうのが、

当時の私の感想でした。

 

だって、なんも解説してないじゃん。

 

慣性力が、

 

を盲目的に

使っていればいい理由って？

 

なんで「慣性力」をなった途端に、

図とか日常生活の例とかでフワッと解説されるの？

 

もっとロジカルに、

理屈でわかるような説明があっていいんじゃ・・・？

 

と白滝は思うわけです。

 

解説がアヤフヤなんですよ。

 

だから、

何に基づいて解けばいいのか、わからなくなる。

 

私が高校時代に「慣性力？？？？？」ってなったのも、

どこ探してもロジカルな解説がなかったから。

 

使うと問題が解きやすいのは、わかる。

 

式を立てるのがラクになる、んだよね？

 

でも、

その慣性力ってのはどこから生まれた？

 

ってのは、

電車がーとか、バスがーとかしか言ってくれないわけですw

 

え？

 

説明になってないじゃん？

 

ということで、

今回は「慣性力をロジカルに解説してみよう」という試みです。

試みというか。

 

今私の手元には、

慣性力を使わずに解いた（慣性力の）問題と解答

があります。

 

良問の風の３６問目。

 

慣性力の問題って、

慣性力を使わずともカンタンに解けるのね！？

 

って驚きました。

 

自分で解いていてですがw

 

慣性力で解く場合は、

を使って「よくわからんけど問題がカンタンになった！」と解くわけですが、

 

使わない場合は、

相対加速度

というものを使います。

 

相対加速度を使って原理的に解くか、慣性力の公式を使ってチート的に解くか、、

みたいな話で。

 

この相対加速度ってやつが、

慣性力の根本。

 

まあ、相対加速度って、

相対速度の加速度版ってだけで。

 

あまり難しくないのよ。

 

そんで、

慣性力が生まれる原因だったりする。

 

たとえばね、

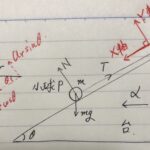
「良問の風３６（２）」では

 

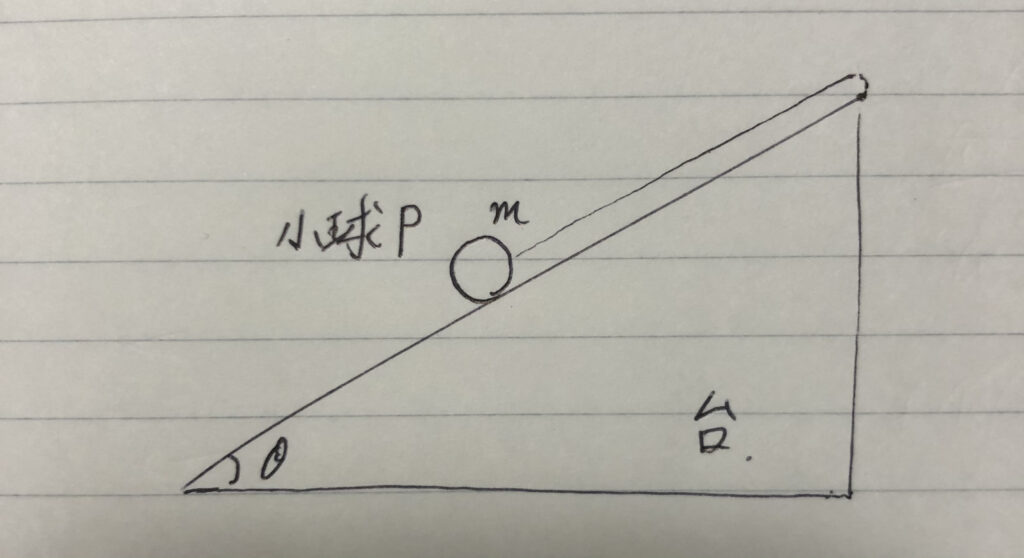
この台が左向きに加速度αで

動いてたりするんですよ。

 

 

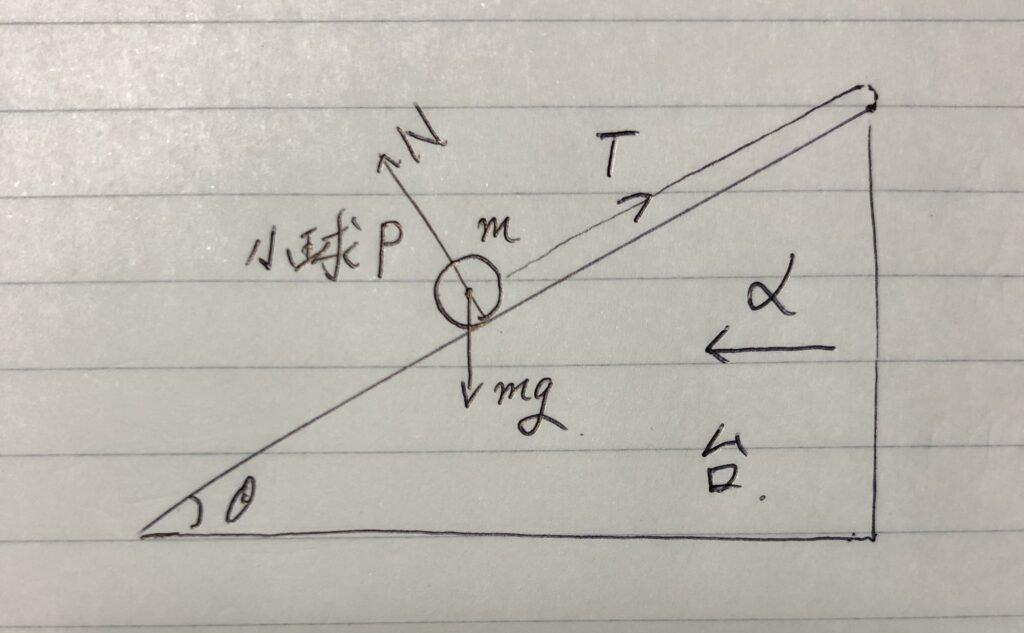
でもさ、

台に動かれると運動方程式が立てにくい

わけね。

 

わかる？

 

このままだと、

小球Pと台の運動方程式を両方立てて、

それを解くことになるんだけど・・・

 

式が複雑になりすぎて無理やねん。

（やってみ？）

 

（台に加速度が働くってことは、その押す力をFと置いて、、）

 

ちなみに問題は、

（良問の風３６問目の（２）ね）

 

だから、

相対加速度か、慣性力を使うのだ。

 

まあ、慣性力の問題だし。

 

でもね、

今回は相対加速度を使って解いてみる。

 

大丈夫、

普通にわかる話しかしないから。

 

やりたいことはね、

ただ１つ。

 

相対加速度を使って、

小球Pから「台の加速度α」を引っこ抜くのだ。

 

わかるかい？

 

小球Pから台の加速度αを抜けば、

台が静止しているように見ることができる。

 

つまり、

 

小球Pは台の加速度を

考えなくて済むようになるのだよ。

 

小球Pの本当の加速度をα_r、

小球Pから台の加速度を引っこ抜いた「見かけの加速度」をωと置くと、

 

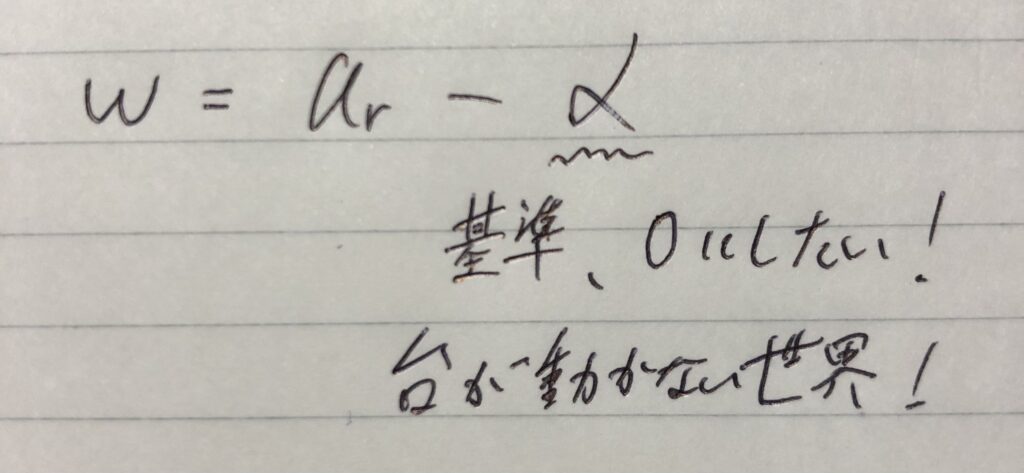
と定義できる。

 

これで、

小球Pから「台の加速度α」を引っこ抜くことができた。

 

これが、

相対加速度ってやつ。

 

小球が台に対して静止していたら、

この「見かけの加速度ω」は０。

 

でも、

今回は小球が台を登ったり、降りたりする可能性があるわけね？

 

わかる？

 

だから、とりあえずωと置いたまま。

 

オーケー？

 

そしたら、

まずは普通に小球の運動方程式を立てる。

 

小球の本当の加速度はをα_r。

 

これを使って、

いつも通りに運動方程式を立てるわけだ。

 

（１）注目する物体を１つに決める。

 

もちろん、小球Pに決める。

 

（２）注目する物体に働く力を、すべて書き出す。

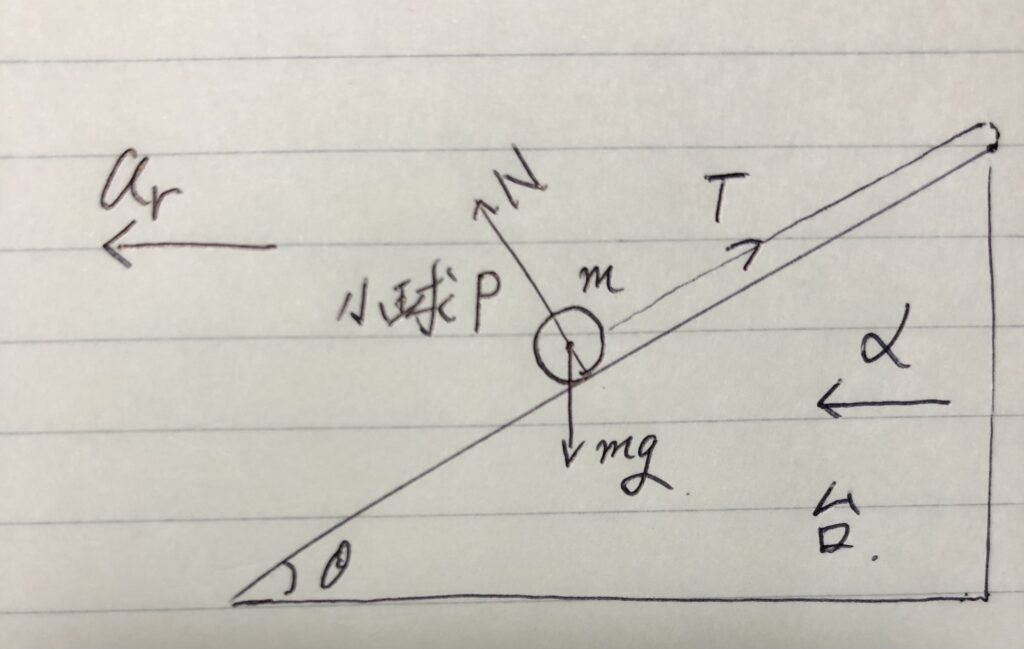
もう書いてある。（垂直抗力Nと張力Tと重力mgだね）

 

（３）X軸とY軸を設定する。

 

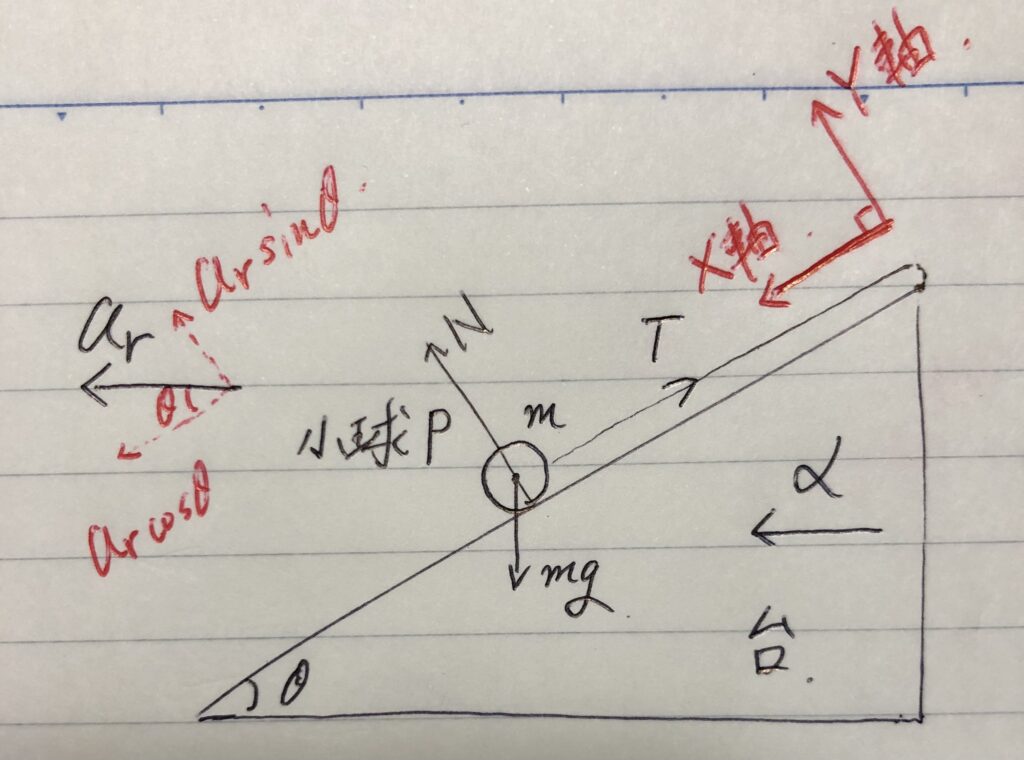
斜面下向きをX軸の正方向、斜面垂直上向きをY軸の正方向と置いた。

 

すると、

小球Pの「本当の加速度α_r」も分解するんだね。

X軸方向：α_rcosθ

Y軸方向：α_rsinθ

 

（４）力を分解する。

 

今回は、重力mgだけが分解だね。

 

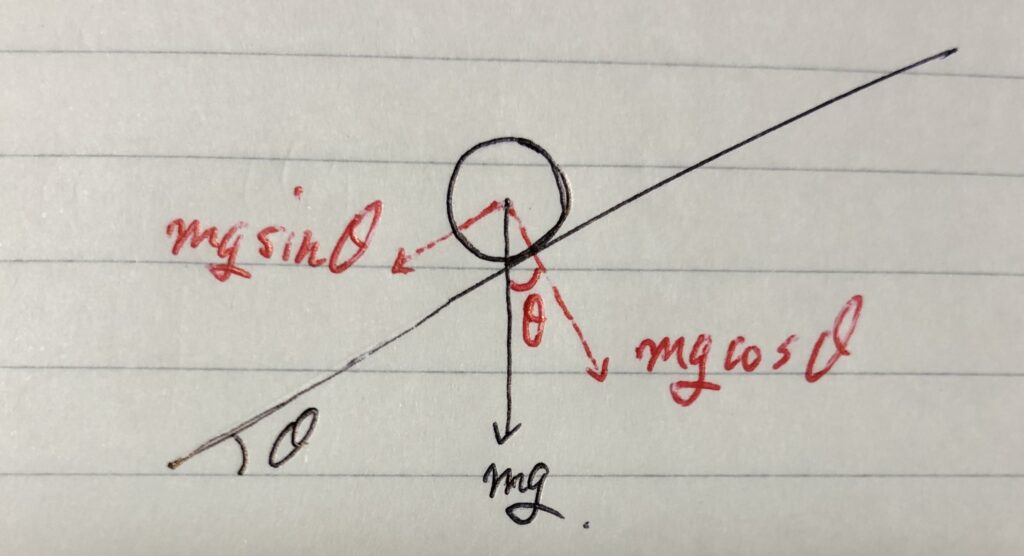
いつものように、

X軸方向：mgsinθ

Y軸方向：−mgcosθ

と分解すればOK。

（mgcosθは負の方向ですね）

 

（５）運動方程式「ma=F」を立てる。

 

X軸方向、Y軸方向それぞれで、加速度と力を代入します。

 

X軸方向：m×(α_rcosθ) = mgsinθ − T

Y軸方向：m×(α_rsinθ) = −mgcosθ + N

 

これで、とりあえず準備が完了しました。

 

（６）小球Pから「台の加速度α」を引っこ抜く。

 

ここからです。

 

小球Pの本当の加速度をα_r、

小球Pから「台の加速度α」を引っこ抜いた「見かけの加速度」をωと置いて、

 

ω ＝ α_r − α

 

と置きましたよね？

（ωを「小球の本当の加速度」α_rと「台の加速度」αで定義した）

 

これで、

小球Pから「台の加速度α」を引っこ抜けたのですが、

 

ω ＝ α_r − α

は変形すると、

α_r ＝ω + α

となりますよね？（入れ替えてα_r の式にしただけ）

 

ここからは、

「台の加速度が０」のように見たいので、

α_r  を消してωの式にしたいのです。

 

だから、

α_r ＝ω + α

を運動方程式に代入。

 

すると、、

 

はい、完成しましたね！

 

X軸方向：mωcosθ = mgsinθ − T − mαcosθ

Y軸方向：mωsinθ = −mgcosθ + N − mαsinθ

 

慣性力を使って出す式と、

同じ式が導出できました。

（−mαcosθ、−mαsinθが慣性力と呼ばれるやつです）

 

どうでしょう？

 

慣性力の公式

 

ってのは、ずいぶんと簡略化されている。

 

まあ、使えるならいいけれど、

いざ使うとなると戸惑いますよね？

 

この力の書き方で、、本当にいいの？

 

なにか、例外はないの？

 

って。

 

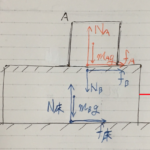
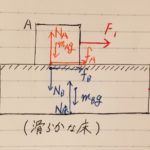
今回解いた問題は、

という問題。

 

台が、斜めっているんだなあ。

 

まあ、本当に慣性力を使い慣れていたら、解けなくもないけれど、、ね。

 

私は、

ちゃんとロジカルに１個ずつ、解いていってもいいと思うのです。

 

だってさ、

大学入試って（１）をミスったら、その先も０点だよ？

 

「はいはい、慣性の法則ね、、あ、あれ？、、えと、これで合ってるのか？、、まあ、やるしかない、、えいやっ！」

って解いてミスってたら、終わりです。

 

死亡。

 

ふつーに（１）から慣性の法則を聞いてきたりするので、

事故死します。

 

（１）から、

「小球Pにはたらく慣性力の大きさを答えよ（X軸、Y軸にわけて）」

とか。

 

「−mα」とか、そんなカンタンには答えさせない。

 

X軸とY軸が指定されて、

分解された慣性力を聞かれるわけね、たとえば。

 

そして、

床が斜めっていたりする。

 

は？

 

でしょ、そんな問題に出遭ったら。

 

もちろん、

でも解ける人はいる。

 

ちゃんと慣性力の本質がわかっているなら、

公式でも迷わず解けるでしょう。

 

でもね、、

普通はそうは行かないんだなあ、、笑

 

だからね、私は、

ちゃんとロジカルに１個ずつ、解いていってもいいと思うのですよ。

 

公式に頼るよりも、

１００％安心だから。

 

まずは加速度を分解してね、

α_r ＝ω + α

って、

本当の加速度α_r を「みかけの加速度ω」と「台の加速度α」の和にする。

 

それを運動方程式

X軸方向：m×(α_rcosθ) = mgsinθ − T

Y軸方向：m×(α_rsinθ) = −mgcosθ + N

に代入して、

X軸方向：m×(ω + α)cosθ = mgsinθ − T

Y軸方向：m×(ω + α)sinθ = −mgcosθ + N

 

X軸方向：mωcosθ + mαcosθ = mgsinθ − T

Y軸方向：mωsinθ + mαsinθ = −mgcosθ + N

って「台の加速度α」を取り外しちゃうんだ。

 

すると、

「台の加速度αがない世界」での小球Pの加速度ω

で考えられるんだね。

 

そのときに。

 

その世界において、

小球Pになぜか働くナゾの力

が慣性力なんだ。

 

わかる？

 

つまりは慣性力というのは、

本当の加速度α_rから「台の加速度α」を引っこ抜く

ための力なんです。

 

そんだけ。

 

それを「相対加速度」を使って計算すると、

 

X軸方向：mωcosθ = mgsinθ − T − mαcosθ

Y軸方向：mωsinθ = −mgcosθ + N − mαsinθ

って導出できて、

− mαcosθ、− mαsinθの部分が「慣性力」ってわけ。

 

ね？

 

ロジカルでしょう？

 

最後に、問題を最後まで解いてみると

 

X軸方向：mωcosθ = mgsinθ − T − mαcosθ

Y軸方向：mωsinθ = −mgcosθ + N − mαsinθ

 

の「ω = 0、T = 0」の時のαが欲しいらしいから、

 

X軸方向：m×０×cosθ = mgsinθ − ０ − mαcosθ

Y軸方向：m×０×sinθ = −mgcosθ + N − mαsinθ

 

X軸方向：０ = mgsinθ  − mαcosθ

Y軸方向：０= −mgcosθ + N − mαsinθ

 

まずは、X軸方向の運動方程式から

α = gtanθ

とわかる。

 

そんで、垂直抗力Nも欲しいらしいから、

Y軸方向の運動方程式に、今求めたαを代入して、

 

N = mg/cosθ

 

って解けるんだね。

 

 

以上っす！

 

慣性力は、

相対加速度で解いた結果を公式化したもの

って覚えておいてくれればいいっす！

 

では！