
(https://www.dnc.ac.jp/albums/abm.php?d=771&f=abm00005964.pdf&n=2025_op_39_butsuri.pdf)
ーーーーーー
仕事は$W=Fx$、$F=PS$だから、$W=Fx=(PS)x=P(Sx)=PV$
(積分が理解できるなら、より正しくは、)
仕事は$W=∫Fdx$、$F=PS$だから、$W=∫Fdx=∫(PS)dx=∫P(Sdx)=∫Pdv$
ーーーーーー
ってことで、要は
$p-V$グラフの面積が仕事$W$
なんですな。(教科書知識)
よって、
気体が外部にした仕事は、「過程Ⅱ」の方が大きい。
また、気体の内部エネルギーは常に、
$U=nC_vRT$だから、
内部エネルギーの変化は、
$ΔU=nC_vRΔT$であるため、
内部エネルギー変化は温度だけで決まる。
(教科書知識)
過程Ⅰも過程Ⅱも、
始点(状態C)と終点(状態A)が同じだから、
最初の温度と、終点の温度も同じ。
よって、内部エネルギーの変化も同じ。
→答え⑧
(以下、Gemini3の解答)
この問題は、P-Vグラフ(圧力と体積のグラフ)を用いて、内部エネルギーの変化 ($\Delta U$)、気体がした仕事 ($W$)、吸熱量 ($Q$) の大小関係を比較するものです。
解説
1. 内部エネルギーの変化 ($\Delta U$) の比較
-
内部エネルギー $U$ は、気体の状態(温度)だけで決まる状態量です。
-
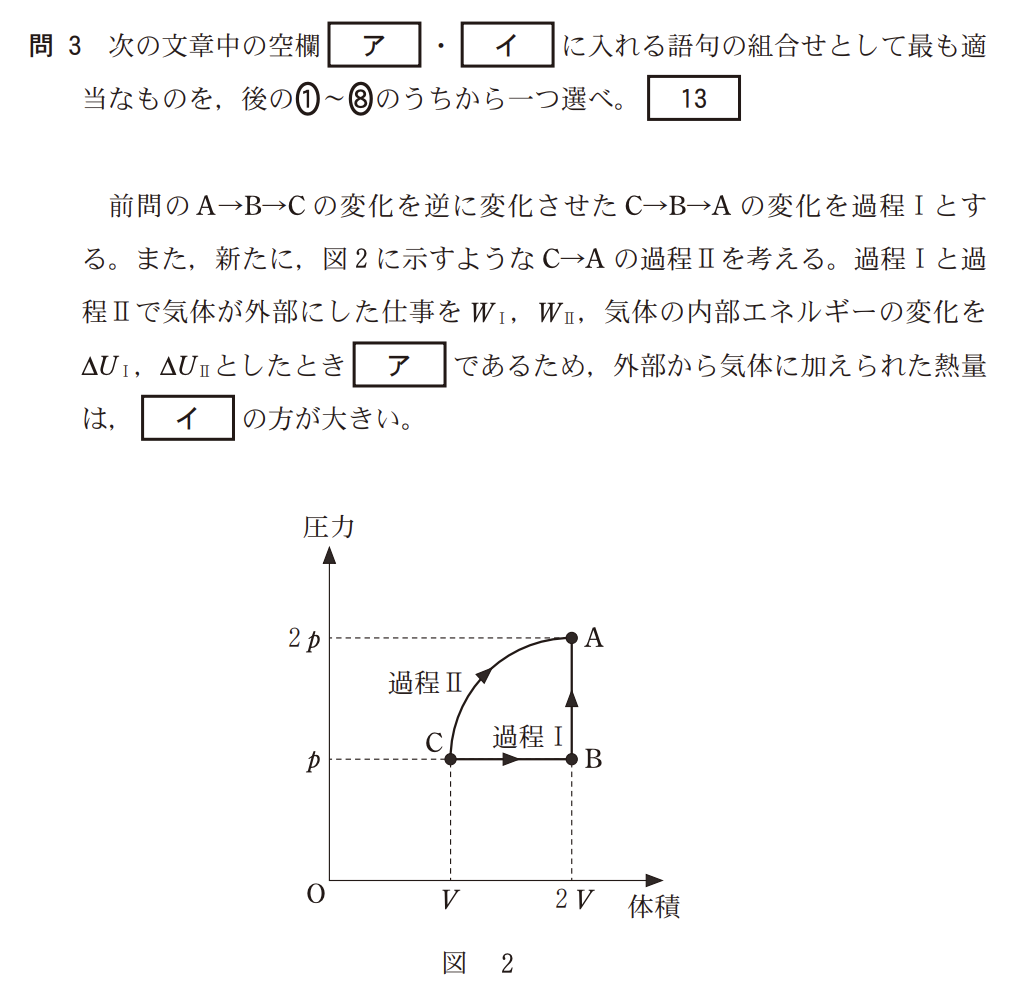
過程Ⅰ(C→B→A)も過程Ⅱ(C→A)も、始点(状態C)と終点(状態A)が同じです。
-
始点と終点が同じであれば、途中の経路に関係なく、内部エネルギーの変化量は等しくなります。
$$\Delta U_{\text{I}} = \Delta U_{\text{II}}$$
2. 気体がした仕事 ($W$) の比較
-
P-Vグラフにおいて、気体が外部にした仕事 $W$ は、グラフの線と横軸(体積軸)で囲まれた部分の面積に相当します。
-
過程Ⅰ(C→B→A):
C→B(圧力 $p$ で体積が増加)の直線の下側の面積(長方形)が仕事になります。B→Aは体積が変わらないので仕事は0です。
-
過程Ⅱ(C→Aの曲線):
図2を見ると、過程Ⅱの曲線は、過程Ⅰの経路(C→B)よりも上側を通って膨張しています。
-
比較:
グラフが上にあるほど、囲む面積(=仕事)は大きくなります。したがって、過程Ⅱの方が面積が大きいため、仕事も大きくなります。
$$W_{\text{I}} < W_{\text{II}}$$(あるいは $W_{\text{II}} > W_{\text{I}}$)
3. 熱量 ($Q$) の比較(空欄 [イ])
-
熱力学第一法則の式は $Q = \Delta U + W$ です。
-
ここで、
-
$\Delta U$ は同じ($\Delta U_{\text{I}} = \Delta U_{\text{II}}$)
-
$W$ は過程Ⅱの方が大きい($W_{\text{I}} < W_{\text{II}}$)
-
-
そのため、足し合わせた熱量 $Q$ も、仕事が大きい過程Ⅱの方が大きくなります。
$$Q_{\text{I}} < Q_{\text{II}}$$
結論
-
[ア]: $\Delta U_{\text{I}} = \Delta U_{\text{II}}$ かつ $W_{\text{I}} < W_{\text{II}}$
-
[イ]: 過程Ⅱ
この条件を満たす選択肢は ⑧ です。
正解: ⑧