(https://www.u-tokyo.ac.jp/content/400239120.pdf)
どうも、白滝です。
電子が動くと、磁場ができる。
これは、電磁誘導の逆(電流の磁気作用)ですね。
そして、この磁場の計算は
大学レベルの積分計算が必要なため、
高校では、たった3通りの答えを教えられますね。
| 直線電流 |
$$H = \frac{I}{2\pi r}$$
|
| 円形電流 |
$$H = \frac{I}{2r}$$
|
| ソレノイド |
$$H = nI$$
|
-
$I$:電流 $[A]$
-
$r$:距離または半径 $[m]$
-
$n$:単位長さあたりの巻き数 $[回/m]$ ($n = N/L$)
そう。
高校物理って、
電流から磁場を計算するときは、
たった3通りの「答え」しかない。
いいですか?
ここまで付いてこられてますか?
まだ、教科書レベルの知識しか、話してませんわな。
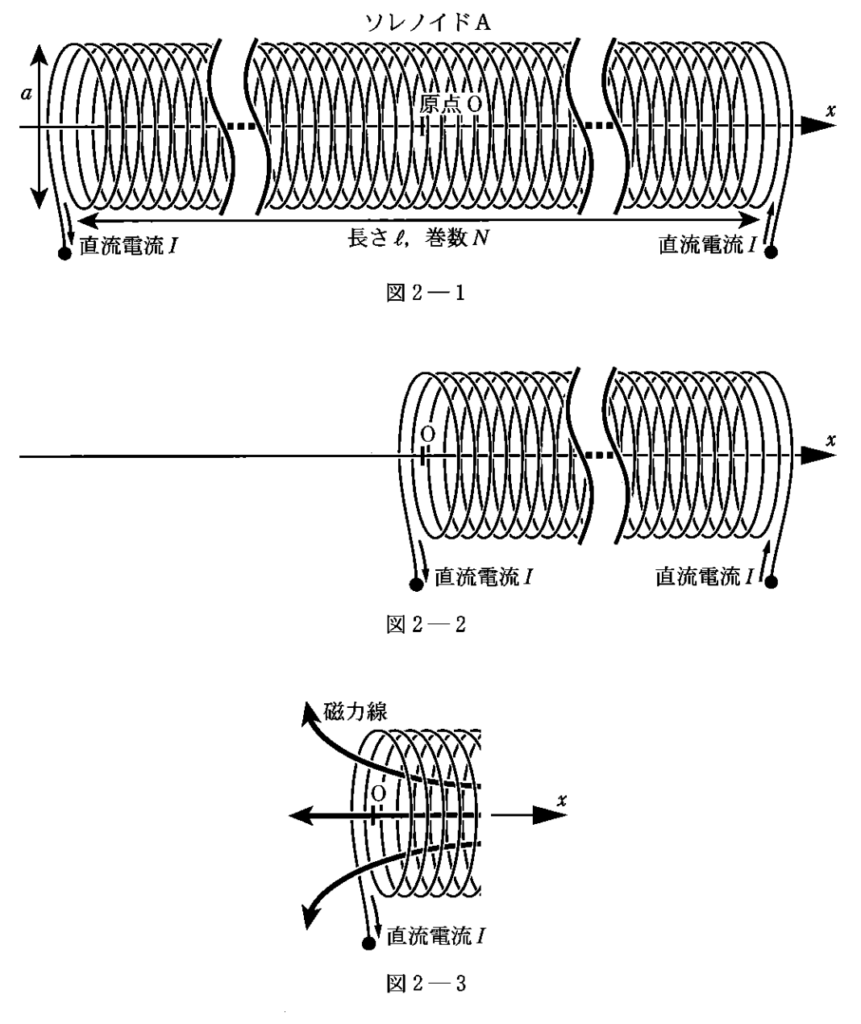
んで、(1)はソレノイドの中心での磁束密度を求める問題なので、
$B=μH$を使えばいいのですな。
$H$は?というと、
ソレノイドの長さ $L$ が、その半径 $r$ に比べて十分に大きい($L \gg r$)と問題文にあるため、
(=ソレノイドの両端の影響を無視できる)
これは教科書通りの「無限に続くソレノイド」とみなせて、
$H = nI$
が使えますね。
また、$n$は単位長さあたりの巻き数ですから、
$n=N/l$と表せる。
すると・・・
答えはもう、計算できますわな。
ええ。
必要な知識は、
ソレノイドの式($H = nI$)が使える条件だけ。
=======
【ソレノイドの重要知識】
ソレノイドの式($H = nI$)が使える条件:
①ソレノイドの長さ $L$ が、その半径 $r$ に比べて十分に大きい($L \gg r$)
または、「ソレノイドの両端の影響を無視できる」と書いてある
または、「「無限に続くソレノイド」とみなせる
(全部同じ意味)
②ソレノイドの内部であること(内部の磁場はどこでも同じ「$H = nI$」)
外部の磁場はゼロ
=======
そう、ただの知識。
知識を聞いているのですわ。
(2)も同じです。知識はちゃんと整理できているか?と聞かれている。


十分長いソレノイドを半分にした、その端の話。
端っこなので、
ソレノイドの式($H = nI$)
が使えないのがミソですね。
使いたい式が使えない。
というか、
その端っこの磁場を導出せよ、という問題ですし。w
ねえ。
式がそのままでは、使えない。
ではどうしようか。
(1)より、
無限に長いソレノイドの磁場は、$H = nI$。
でも、(2)は端っこの話。
図2-3を見ると、
①磁力線は通っているから、端っこの磁場はゼロではない。
②けれども、磁力線は乱れている(=磁力線の密度が小さくなっている)から、磁場は「無限に長いソレノイド($H = nI$)」よりも小さい。
じゃあ、答えは「無限に長いソレノイド($H = nI$)」の半分なのでは?
「無限に長いソレノイド($H = nI$)」を
ちょうど半分にしてますし。w
半分っぽくね?
答えって、$B_1=1/2 B_0$じゃね?
だって、高校物理の範囲では
計算できない状況だもの。
んで、ゼロでも「無限に長いソレノイド($H = nI$)」も使えないとしたら、
その中間では?
ねえ。
そうなんでしょう。
そう考えてみると、左右のソレノイドの磁場の和が「$H = nI$」なのでは?
「端」+「端」が、「$H = nI$」となる。
だって、右ねじの法則より、
左のソレノイドも、右のソレノイドも、
磁場の向きは同じで、右向きですから。
この原点$O$を境にして、
左右のソレノイドの「端」の磁場の和が、
$H = nI$となっている。
だから、
片方のソレノイドの「端」の磁場は、
やっぱりその半分なのでは?
というのが、答えです。
ソレノイドの磁場を
「左右のソレノイドの磁場の和」から考える問題だったのですな。
↓
↓
(Gemini3の回答)
(2) 半分のソレノイドによる磁束密度 $B_1$
この問題は**「重ね合わせの理(スーパーポジション)」と「対称性」**を利用すると簡単に解くことができます。
-
元のソレノイドを分割して考える
元の長いソレノイド(長さ $\ell$)は、原点Oを境にして「左半分 ($x<0$)」と「右半分 ($x>0$)」の2つのコイルを直列につなげたものとみなせます。
-
対称性
原点Oはソレノイド全体のちょうど中心にあるため、
「左半分が原点Oにつくる磁場 $\vec{B}_{\text{left}}$」と
「右半分が原点Oにつくる磁場 $\vec{B}_{\text{right}}$」は、
対称性により大きさも向きも等しくなります。
-
重ね合わせ
元のソレノイド全体の磁場 $\vec{B}_0$ は、これら2つの和です。
$$|\vec{B}_0| = |\vec{B}_{\text{left}}| + |\vec{B}_{\text{right}}|$$対称性より $|\vec{B}_{\text{left}}| = |\vec{B}_{\text{right}}|$ なので、今回求めたい右半分による磁束密度 $B_1 (= |\vec{B}_{\text{right}}|)$ を用いると:
$$B_0 = B_1 + B_1 = 2B_1$$ -
結論
よって、半分にしたソレノイドの端(原点O)における磁束密度は、元の中心の磁束密度の半分になります。
$$B_1 = \frac{1}{2} B_0$$