定常波が主ですが、他もまとめました。
波動の全体像です。
どうぞ。
【ここは一直線上での話(1次元)】
最初は、震源が1つの場合。
y-tグラフとは?
y-xグラフとは?
横波と縦波って?
波の反射、固定端と自由端
波を数式で表すと?
定常波:震源が2つになった場合。その合成波を考えていく分野。
(流体摩擦や圧力によって)
震源から伝わった力が
同じ向きで合力が最大→腹
震源から伝わった力が
逆向きで合力が常に0→節
あとは、条件を決めて定常波
を考えるだけ。
自由端:同位相の震源を端を鏡にして逆側、同じ距離におく。端は腹。
固定端:逆位相の震源を端を鏡にして逆側、同じ距離におく。端は節。
弦の振動:両端が節。それだけの定常波。
気体の振動(筒の中)
開管:両端を腹。
閉管:閉じてる方を節、開いてる方を腹。
開口端補正:管の端よりもちょっとだけ腹が飛び出ること。管の長さ+Δxの位置に「腹」と書いておけばいい。
うなり:振動数の引き算。+ーがポイントだね。
ドップラー効果:進言が動いていたら?節となる壁(反射板)が動いていたら?聞く側が動いていたら?の3拍子。2次元の図も出てくるけど、解答は1次元的。
【ここからは、平面で波を考える(2次元)】
波の反射・屈折:異なる媒質に入ったら?波はどうなるのか?→反射or屈折をする。
レンズ
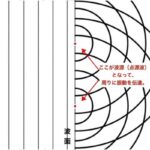
波の干渉:2次元で定常波を考えるってこと。直線上だけでなく、平面で合成波を考える。
ヤングの実験
回折格子
薄膜による干渉
くさび形薄膜による干渉
ニュートンリング
波動はまず、
1直線上で、振源が1つの場合
を学ぶ。
次に、
1直線上で、振源が2つの場合
を学んだんですね。
(これが定常波)
そして、1直線上のよしみで
ドップラー効果がある。
ここまでが、1直線上の波の話。
ここからは、平面で。
2次元で波を考えていく。
最初は、波の反射と屈折ですね。
「曲がる」ってのは2次元じゃないとできないので、屈折を考えました。
媒質が変わる→波の伝達速度(波の「波形」が進む速さ)が変わる→定常波で作られた「波面」が曲がる
んでしたよね?
媒質を伝達する波の速さって、その媒質の「種類」と「温度」のみに依存しますから。
次に、波の干渉です。
これは、完全に2次元(平面)で定常波を考えにいってます。
1次元から2次元になると、いろんな現象が起こるんだなあ・・・
以上。