どうも、白滝です。
慣性力で非常にお困りかと思われます。
私も大学入試のときですら、
慣性力に悩まされた身です。w
めっちゃ難しい。
わからなすぎて、エグい。
そう思ってネットで色々調べても、
なーんか掴みにくいんですよね。。
物体がそのままの状態を続けようとする性質を「慣性」という。力が働いていない物体が、静止ないし等速直線運動をするのが「慣性の法則」だ。
ある観測基準(これを「座標系」と呼ぶ)にとって、「慣性の法則」が成り立っているとき、観測者のいる座標系は「慣性系」と呼ばれる。慣性系においては、物体には力に比例した加速度が生じる。
ところが、慣性系に対して加速度運動する座標系では、「慣性の法則」が成り立たない。
慣性系で静止ないし等速直線運動する物体に対して、加速度運動する観測者が見れば、逆に加速度運動して見える。力が働いていない物体が、加速度運動するのだから、「慣性の法則が成り立っていない」というわけだ。
ところが、同じ観測者が、あくまで慣性の法則が成り立っていると考えたらどうなるだろう。
「加速度が生じているのだから、力が働いている」と考えたとしてもおかしくはない。急ブレーキをかけた電車内で前につんのめるとき、「前に力が働いた」と考えた方が自然なこともある。これが「慣性力」であり、「どうしてスペースシャトル内では、無重力になるのだろうか?」で扱った「見かけの力」の正体だ。
(https://humans-in-space.jaxa.jp/faq/detail/000706.html)
JAXAでもわかりやすく解説しようとしてますが、
理解しずらかったです。
うん。w
あのさ、
ごちゃごちゃ説明とかいいからさ、
慣性力の汎用的な解き方
を教えてよ!!
というのが、当時の私のド爆発。
色々、そんな説明どうでもいいんです。
なんかバスがー、とか、
電車の中の人がー、とか、そんなたとえ話もどうでもいい。
もうさ、
入試で確実に使える解き方・考え方を
教えて欲しい。
ねえ、教えてよ
先生でも、塾講師でも、誰でも
めっちゃ困ってるんだからさ。
そう思うのは、私だけ?
ではないと思うので、
めっちゃ丁寧に解説していきますね
慣性力の本質は・・・
なんか色々省いて、大事なところだけお伝えします。
慣性力の本質は、相対加速度です。
聞いたことはありますか?
相対加速度。
ただの、「相対的な」加速度です。
相対速度は扱ったことあるでしょ?
(右に5m/s走る車から、左に3m/sで走る車を見ると、左に8m/sで走っているように見えるよねー、ってやつ)
ブブーン
習ったでしょう。
速度は「視点」を変えることで、数値をいじることができる。
これがめっちゃ大事なこと。
(これが慣性力にめっちゃ繋がります)
右に5m/s走る車と、左に3m/sで走る車があったとして、
その世界の車の速度を全部右に-5m/sしたら、
右に走る車の速度を0m/sにできるでしょ?
(これが相対速度ってやつです)
速度には絶対的な「0」は存在足なくてね、
だいたい地面の速度を「0」に設定しているだけ。
本当は地球は自転しているから、地面も動いているし、
公転もしてるからぐわんぐわん移動してるわけだ。
でも、通常は地面を「0」と基準にしている。
速度も、加速度も。
んでね、
速度って、いじることができる。
全体の速度をいじれば、
ある車の速度を「0」に変更できる。
相対速度でいう、「視点」を変えるってやつですね。
右に走る車の速度を「0」にしたいなら、
その世界の車の速度を全部右に-5m/s
してあげればいい。
そういうことです。
加速度でも、同じことができる。
次は、加速度で考えてみましょう。
加速度にも、絶対的な「0」は存在しません。
だから、世界の加速度はいじることができるのです。
うまーくね。
問題が解きやすいように、
いじることができる。
相対速度と同様に解説すれば、
右に$5m/s^2$走る車と、左に$3m/s^2$で走る車があったとして、
その世界の車の速度を全部右に$-5m/s^2$したら、
右に走る車の速度を$0m/s^2$にできるでしょ?
加速度は「絶対値」じゃないから、
相対的にね、
誰かの加速度を「0」に変えることができる。
(世界の加速度をいっぺんに変更すれば)
で、
誰かの加速度を「0」にしやすくなる問題って、
卓弾あるわけ。
そこで出てくるのが、慣性力なのです。
いいですか
繋がってますよ?
世界の加速度をいじると、
世界中の物体に「追加の加速度」が発生しますよね。
たとえば、
世界の加速度を右に「+a」だけ増やして、
誰かの加速度を相殺($=0m/s^2$)にしたとすると、
もちろん他の物体には、
右に「+a」の加速度が追加されたままですよね?
でもこれって、
世界中の物体に
物体の質量×「+a」の力がかかった!
とも言えますよね!?
(この力が慣性力)
あれです、運動方程式。
ma=Fの計算式の通り、
「追加の加速度」は「追加の力」に変換して
考えることができるんです。
加速度に「その物体の質量」をかければ、
その物体にかかる力になる。
一部の加速度だけ抜き出して、
その加速度だけを「力(F=ma)」に変換もできるんです。
それをね、
物理の教科書では、
「慣性力」なんてカッコつけて言っちゃってる。
いい?
慣性力は元々、
世界の加速度をいじって、世界中の物体に生じた加速度
なんです。
その生じた加速度に、その物体の質量をかけて、
「力」として表現しただけ。
それが慣性力の正体。
めっちゃ「本質」がわかりにくいアレ(慣性力)
の正体です。
ではたとえば、バスの中のバネとか考えちゃいましょうか。
ぷらーん、ぷらーん、と。
右に加速してるバスの天井から、
バネで物体がぶら下がっているとしましょう。
a
→

このバスの中で、
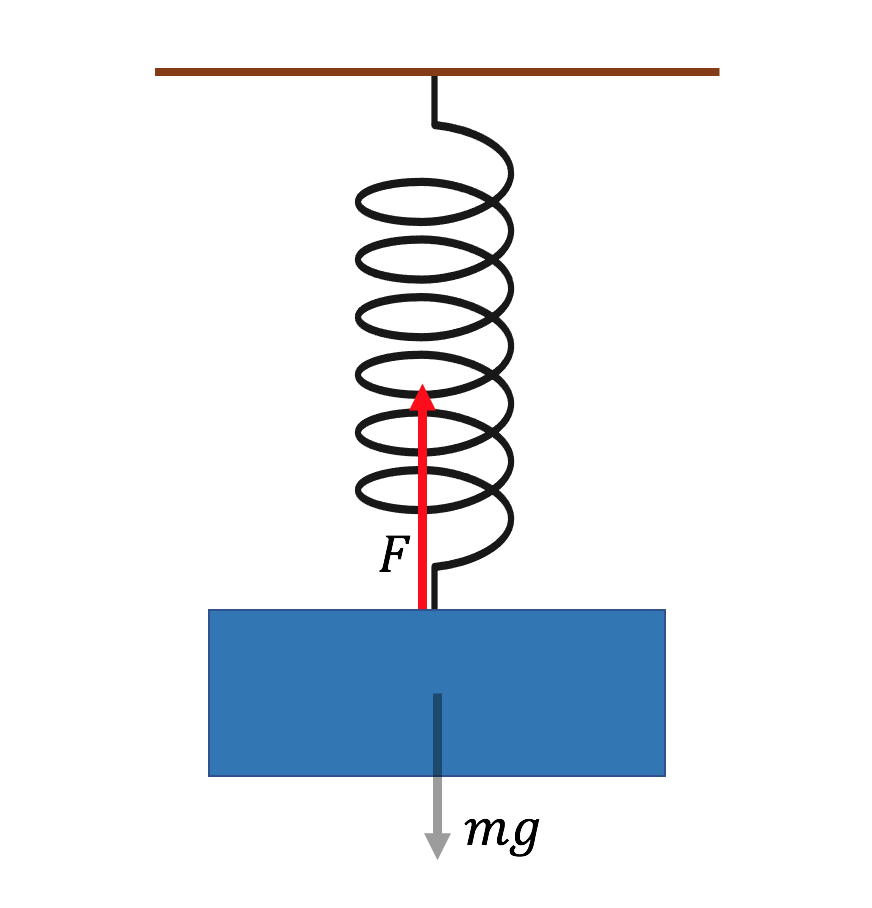
バネで物体が吊り下がっている。
そして、バスは右(正方向)に+aで加速しているとしましょう。
その状態の時の、
物体がバネから受ける力Fを求めたい、
みたいな問題。
入試にも出る形式ですね。
うわあ・・・
そう。
解いたことがある人はわかるんですけど、
そのまま解くのはかなり大変で。
もしそのまま解くなら、
バスと「バネと物体」の運動方程式
をそれぞれ立てて
連立しないといけないんですが、、
これが難しい。
なんでかっていうと、
バスが加速しているから。
バスの加速がやだ。
めっちゃ考えずらい。
式が立てずらい。
じゃあ、、
どうすれば、、
世界中の加速度を「-a」して、バスの加速度を0にすればいい!!
そうです。
これが今回の話なのです。
バスは右に「+a」で加速しているのですから、
世界中の加速度を「-a」すれば「0」になりますよね!?
バスが止まっている、とみなせますよね!?
そんな世界、
めっちゃ計算が楽だと思いませんか?
a=0

その代わりに、
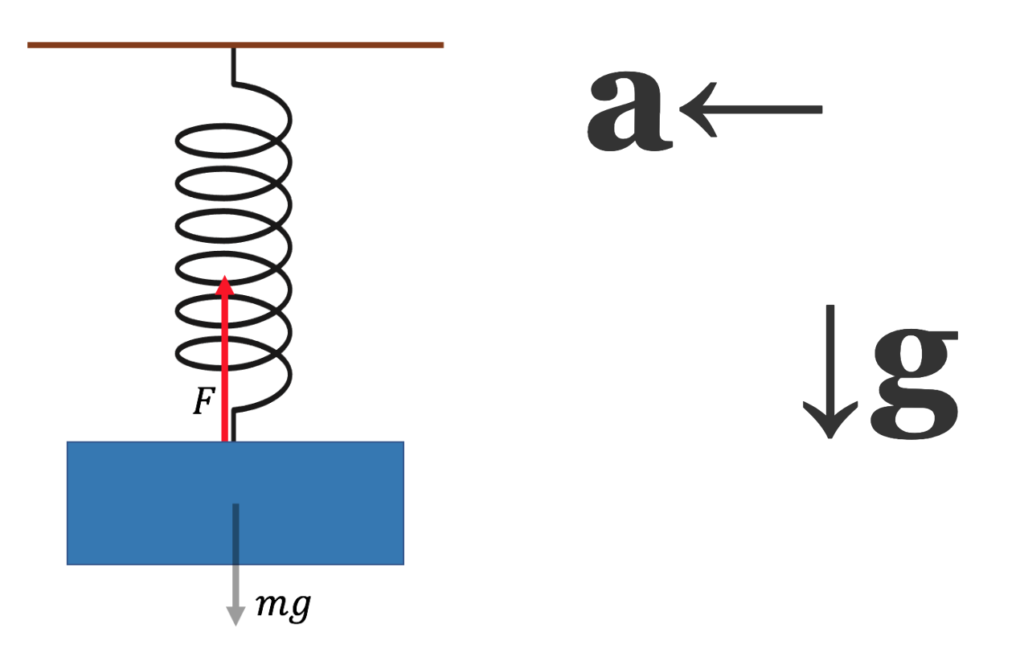
世界の加速度が(右を正とすると)「-a」される!!
というのが、
めっちゃ大事な話。
この世界で青い物体(質量m)を考えるとすると、
重力加速度gだけではなく、左向きにもaの加速度がかかっている!?
という世界になるわけ。
(この「a」は重力加速度と同じような扱い)
ね?
で、この左向きにかかった加速度「a」に青い物体の質量mをかけると、
ma
と「追加の加速度」を「力」で表せるってこと。
それを慣性力と呼ぶってこと。
あとは自分で手を動かして学んで、ってこと。
以上。
もっと知りたいことがあれば、
メルマガまで来てください。
色々お答えしてます。
では