(https://www.dnc.ac.jp/albums/abm.php?d=771&f=abm00005964.pdf&n=2025_op_39_butsuri.pdf)
どうも、白滝です。
これも、問うているのは「習った知識」の確認ですね。w
- 力の分解と合成
- モーメントの知識
ちゃんと覚えてますか。
手を動かせますか。
ただ、それだけの問題。
具体的には、
- 力の分解と合成→力の大きさを求める
- モーメントの知識→合力の位置を求める
って作業ですわ。w
大丈夫ですか?
ちゃんと「知識」は揃ってますか?
まずは、力の分解と合成から
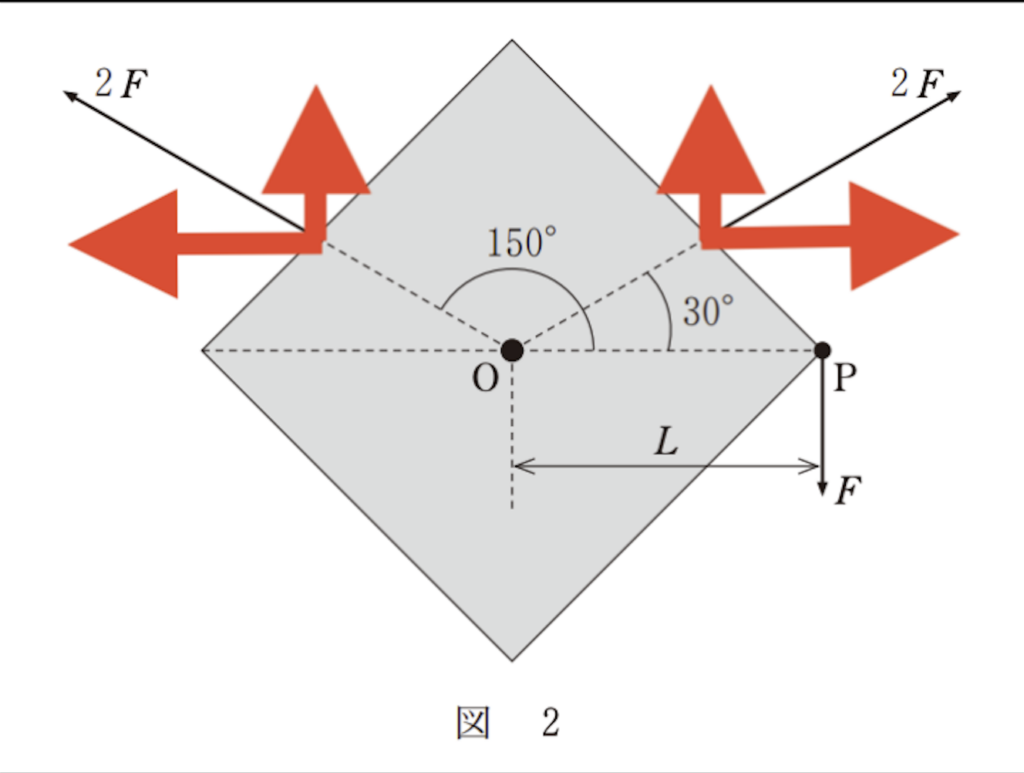
力の分解はご存じのとおりで、
この赤矢印の「水平方向」の力は
打ち消しあうのが分かりますよね。
(選択肢を見ても、水平方向の力はない)
だから、縦方向の力のみを考えればよい。
【縦方向】
赤矢印:上向きの$F$が2本
黒矢印:下向きの$F$が1本
だから、足し算すると、
合力は上向きのの$F$になるはずですね!
あとは、モーメントの知識から。
力のモーメントとは、
「回転軸を通る直線」に垂直な力
で計算するのでしたね。
(復習なのでさらっと)
そんで、メルマガでもお話ししましたが、
モーメントは自分で回転軸を設定する
のがルールでした。
じゃあ、
ここでは点Oを回転軸に設定して・・・
問題の図2にある「黒の$2F$の矢印」は、
2本とも「回転軸を通る直線」に平行だから・・・
「黒の$2F$の矢印」は、力のモーメントに影響しない
ことがわかるかと思います。
だから、残る力は点Pにある「$F$の矢印」だけ。
点Oを回転軸に設定したことを忘れずに、
モーメントを計算すると、
反時計回りに$FL$という値になりますね。
で、
もちろん「合力」も、
同じモーメントを持っていないとオカシイですから、
(だって、合力ですから。たし合わせただけで、同じ話をしてますから)
求める「合力」も、
モーメント「反時計回りに$FL$」を持っている
ことになる。
いいですか?
ここまでに計算した「合力の情報」をまとめますと、
- 大きさは「上向きに$F$」
- モーメントは「点Oを回転軸にして、反時計回りに$FL$」
じゃあ、これらに当てはまる、
位置と力のおきさを、図に描くと・・・
というのが、答えです。
ええ。
じゃあ、細かな解答は、
AIにでも任せましょうか。
(Gemini 3)
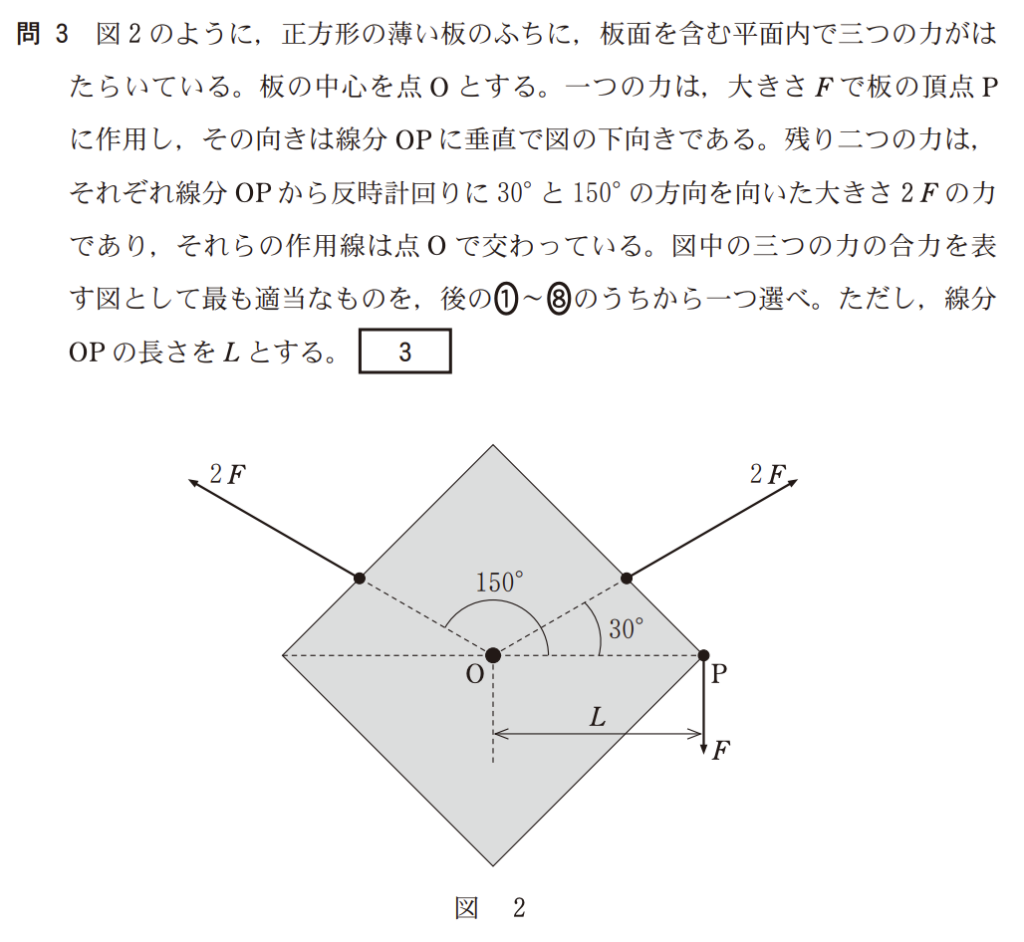
この問題は、**「力のベクトル和(大きさ・向き)」と「作用線の位置(モーメントのつり合い)」**の2段階で考えるのがポイントです。
解答へのステップ
1. 点Oにはたらく2つの力($2F$)を合成する
まず、点Oを中心にはたらいている2つの力(大きさ$2F$)に注目します。線分OPを基準(x軸)として考えます。
-
右側の力($30^\circ$):
-
OP方向成分(横):$2F \cos 30^\circ$
-
OPと垂直な方向成分(縦):$2F \sin 30^\circ = 2F \times 0.5 = F$ (上向き)
-
-
左側の力($150^\circ$):
-
OP方向成分(横):$2F \cos 150^\circ = -2F \cos 30^\circ$ (右側の力と逆向きで打ち消し合う)
-
OPと垂直な方向成分(縦):$2F \sin 150^\circ = 2F \times 0.5 = F$ (上向き)
-
結果:
点Oにおける2つの力の横成分は打ち消し合ってゼロになり、縦成分(上向き)だけが残ります。
その大きさは $F + F = \mathbf{2F}$ です。
つまり、**「点Oに、OPと垂直な上向きに大きさ$2F$の力がかかっている」**のと同じことになります。
2. 全体の合力を考える
次に、先ほど求めた力と、点Pにはたらく力を合わせます。現状は以下のようになっています。
-
点O: 上向きに $2F$
-
点P: 下向きに $F$ (点Oから右に距離 $L$ の位置)
これらは平行で逆向きの力です。
-
合力の大きさ: 上向き$2F$ - 下向き$F$ = 上向き $F$
-
合力の向き: OPに対して垂直で上向き(図の上方向)
3. 合力の作用線(位置)を求める
最後に、この合力が「どこ」にはたらくかを求めます。
力のモーメント(回転させる働き)のつり合いを利用します。点Oを基準に考えましょう。
-
元の力が点O周りに及ぼすモーメント:
-
点Oの力($2F$):距離が0なのでモーメントは 0
-
点Pの力($F$):距離 $L$ で下向きに引くので、時計回りに $F \times L$
-
合計モーメント: 時計回りに $FL$
-
-
合力が及ぼすモーメント:
-
合力は「上向きに $F$」です。
-
これが「時計回りに $FL$」のモーメントを持つためには、点Oのどちら側にあればよいでしょうか?
-
点Oより左側にあれば、上向きに引くことで時計回りの回転力が生まれます。
-
距離を $x$ とすると、モーメントは $F \times x$ です。
-
$F \times x = F \times L$ より、$x = L$ となります。
-
結論
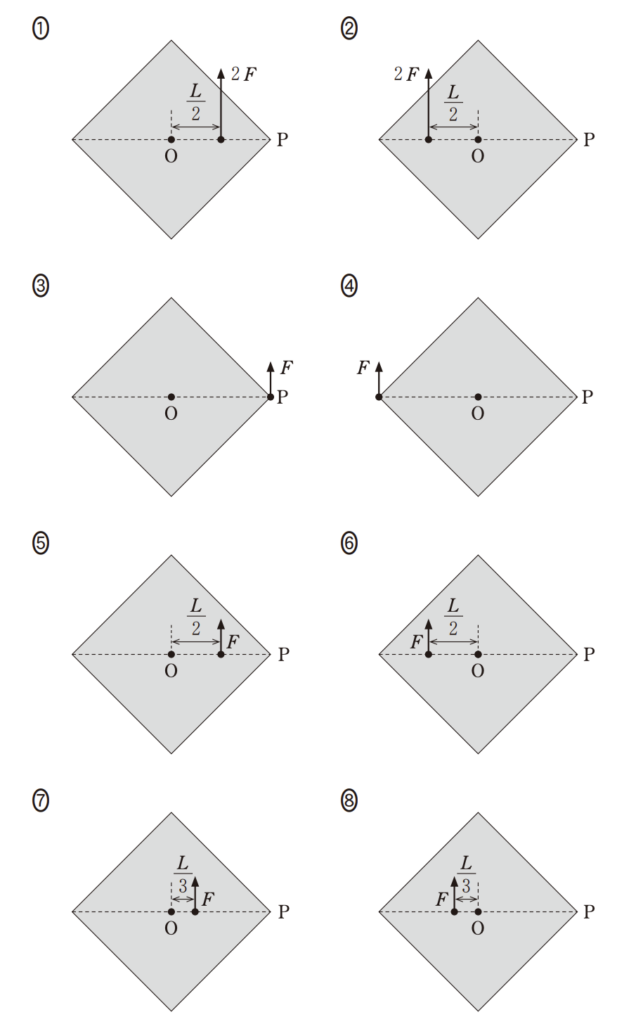
これまでの計算から、求める合力を表す図の条件は以下の通りです。
-
大きさ: $F$
-
向き: OPに垂直で上向き(図の上方向)
-
位置: 線分OPの延長線上、点Oから左へ距離 $L$ 離れた点
正解の図の特徴:
点Oの左側(点Pと反対側)に、点Pと同じ距離だけ離れた位置から、上向きに矢印(長さは点Pの矢印と同じ)が伸びている図が正解となります。
(・・・続く)