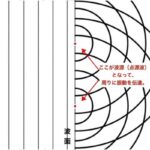
波の干渉は「経路差」の問題。
だから、
「経路差=波長の整数倍」なら、強め合う。
「経路差=波長の整数倍+λ/2」なら弱め合う。
を使っているだけなんだ。
この「経路差」が違うだけ。
この「経路差」を求める方法が
異なるだけ。
やってることは、
ぜーんぶ同じ。
その点に届いた波の位相が同じ→強め合う。
その点に届いた波の位相がπズレている→弱め合う。
ってのを計算してる。
強め合う点の位置を求めて、その点の間隔を求めて・・・
という作業ですね。
それを波長で表すと、
「経路差=波長の整数倍」なら、強め合う。
「経路差=波長の整数倍+λ/2」なら弱め合う。
ってだけ。
これを各場合において考えるのが、
波の干渉。
ぜんぶ、同じ作業をしてるんだ!
経路差を求める作業だけ、ちょっと違うコツがいるだけなんだ!
とわかれば、大丈夫。
以下、まとめです。
【2つの波源による干渉】
ヤングの実験。
回折格子。
【1つの波源と反射による干渉】
薄膜、楔形、ニュートンリング。
プラス、薄膜に斜め入射した場合。
ーーーーーーーー
薄ーいとこに光が入ると、
その反射で生まれた波との波長差が小さいから、「強い」波の干渉が起こる。
(目に見えるレベルで)
ーーーーーーーー
ぜーんぶ、
やっていることは同じです。
「経路差=波長の整数倍」なら、強め合う。
「経路差=波長の整数倍+λ/2」なら弱め合う。
これを、
ひたすら計算しているのだ。
この「経路差」の求め方が
違うだけで、
やってることの本質は
同じなのだわな?
だから、
この「経路差」の求め方を。
とっとと覚えてしまおうよ。