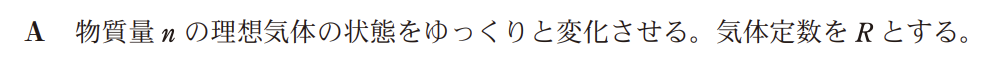
(https://www.dnc.ac.jp/albums/abm.php?d=771&f=abm00005964.pdf&n=2025_op_39_butsuri.pdf)
ええ。
ただのグラフ変換の問題ですね。
$PV = nRT$ を変形して、
$T = \frac{P}{nR}V$ とし、
ここからA→B、B→Cの時の$T$の変化を見ればOK。
A→B
$P$が減少するので、$T$も減少する。
($nR$と$V$は一定。)
B→C
$V$が減少するので、$T$も減少する。
($nR$と$P$は一定。)
$T = \frac{P}{nR}V$ に沿って減少するので、$T$は$V$に対して、線形に減少する。
※線形に: 直線的に、という意味。
よって、②
↓
↓
(以下、Gemini3の解答)
ご提示いただいた熱力学の問題(問2:T-Vグラフの選択)の解答と解説を作成します。
この問題は、P-Vグラフ(圧力と体積の関係)で示された変化を、**T-Vグラフ(温度と体積の関係)**に変換して考える問題です。
解説
理想気体の状態方程式 $PV = nRT$ を変形した式 $T = \frac{P}{nR}V$ を元に、各過程のグラフの形状を考えます。
1. 過程 A $\rightarrow$ B (定積変化)
-
変化の内容: 体積 $V$ は $2V$ のままで一定。圧力 $P$ が減少($2p \rightarrow p$)。
-
温度 $T$ の変化: 体積が一定で圧力が下がるので、温度は下がります(シャルルの法則)。
-
グラフの形状:
-
横軸(体積)は動きません。
-
縦軸(温度)だけが下がるので、下向きの垂直な線になります。
これにより、選択肢は ①、②、④、⑤、⑥ に絞られます(③は斜めに動いているので除外)。
-
2. 過程 B $\rightarrow$ C (定圧変化)
-
変化の内容: 圧力 $P$ は $p$ のままで一定。体積 $V$ が減少($2V \rightarrow V$)。
-
温度 $T$ の変化:
-
状態方程式 $T = \frac{P}{nR}V$ において、$\frac{P}{nR}$ は定数です。
-
つまり、$T$ は $V$ に比例します($T \propto V$)。
-
したがって、グラフは原点を通る直線(の一部)になります。
-
-
グラフの形状:
-
体積が減るにつれて温度も直線的に下がるため、左下(原点方向)に向かう直線となります。
-
3. 選択肢の検討
過程 B $\rightarrow$ C の形状で判断します。
-
①、⑤: B $\rightarrow$ C が水平(温度一定)になっています。これは誤りです。
-
④、⑥: B $\rightarrow$ C が曲線になっています。比例関係(直線)ではないため誤りです。
-
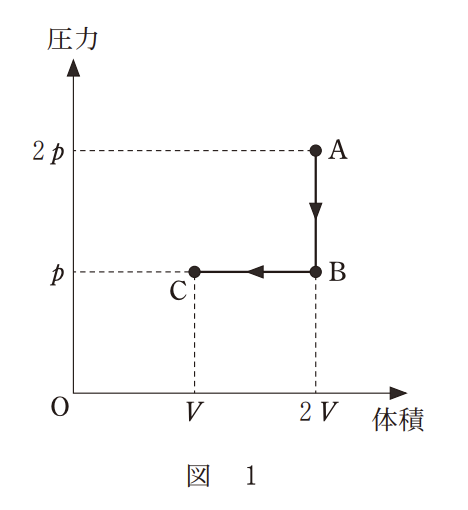
②: B $\rightarrow$ C が原点に向かう直線になっています。これが正しい形状です。
結論
A$\rightarrow$Bで垂直に下がり、B$\rightarrow$Cで原点に向かって直線的に下がるグラフを選びます。
正解: ②







