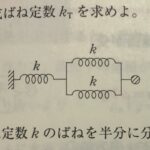
ー滑車の性質のすべてー
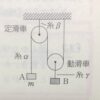
定滑車→糸の張力はどこでも同じ!
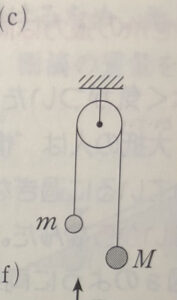
定滑車はそんだけ。
この$m$と$M$にかかる張力の大きさは等しく$T$とおける。
動滑車→糸の張力はどこでも同じ!
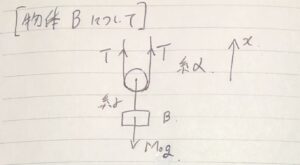
糸が力$T$引かれると、動滑車は上に$2T$で引かれる。
これが、動滑車の基本。
動滑車は、小さな力で「重いもの」を動かすために作られた。
ものを2倍の力で動かせる。
物理の「仕事」の話だね。
$$(仕事)=(力)×(距離)$$
わかるかい?
動滑車は、
人の「力」→ものに伝わる「力」
の間に
仕事(エネルギー)を挟むための道具。
一度「仕事(エネルギー)」に変換することで、
$$(仕事)=(力)×(距離)$$
を使えるようにした。
つまりは、
「距離」を使えるようにしたんだ。
力だけでなく、
「距離」を使ってものを動かす。
これが、仕事の概念。
同じ力でも
動く距離を半分にする
↓
$$(仕事)=(力)×(距離)$$
によって
仕事(エネルギー)が倍になる
↓
伝わる力が倍になる
というように。
言い換えれば、
テコの原理を使えるようにする。
そのための道具なんだ。
だから、
「力」は倍になるけど、それ以外は半分になる。
糸が長さ$l$引かれると、滑車は上に$\frac{1}{2}l$だけ上がる。
糸が速さ$v$で引かれると、滑車は上に$\frac{1}{2}v$で上がる。
糸が加速度$a$で引かれると、滑車は上に$\frac{1}{2}a$で上がる。
「力」は倍になるけど、それ以外は半分。
これが動滑車の性質のすべて。
覚えておいてね。

倍になるのは
何の力?→動滑車が持ち上げられる力。
半分になるのは
何の距離?→動滑車が持ち上げれる距離。
何の速さ?→動滑車が持ち上げられる速さ。
何の加速度?→動滑車が持ち上げられる加速度。