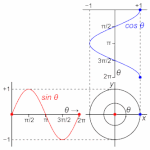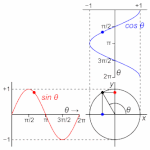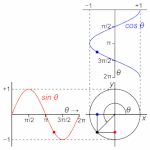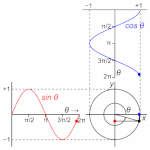
自由端反射は、位相は変わらない。
固定端反射は、位相が+π変わる。
ってどゆこと?
位相が+π変わるって?
なんで、位相を角度で表すの?
って思いますよね。
「+π」って?
なぜ、位相は角度で
表されるのか?
そもそも、位相とは?
・・・・・・
という話を
今回したいと思います。
位相の大元は、周期です。周期と位相に親密な関係がある。
位相とは何か?
それは、
周期の余りだったりする。
1周期、2周期・・・とカッチリじゃなくて、
そのあまりの角度。
それが、位相。
位相の正体。
うん?
なんのこと?
ってかんじですよね。笑
位相とはなにか?
それは、
周期の「途中の角度」をいいます。
周回の途中。
1周期が終わる前の、途中の部分。
うーん?
よくわからない?
昔の物理学者は、1周期を円1周と定義しました。
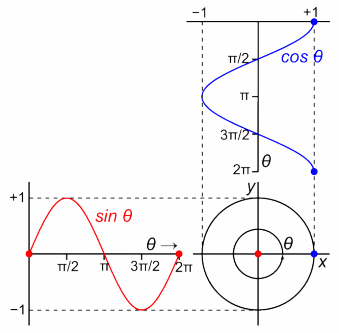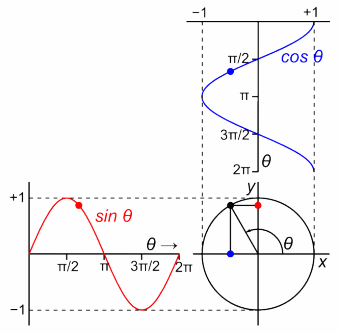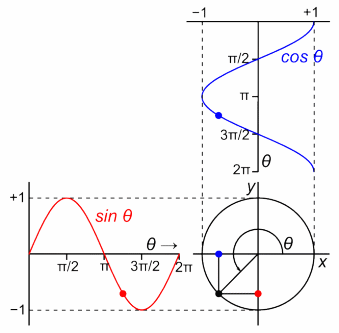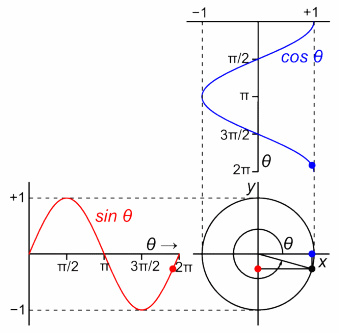
1周期=円1周。
1周期=角度2πを回転すること。
そう定義した。
1周期とは、
数学的には円の1周なのです。
角度を「2π」回転すること
なのですよ。
つまりは、
1周期を角度2πとして、円の1周で1周期を表すことにしました。
そう定義した。
物理学者は、
周期を数学的に定義したんです。
すると、
あまりの角度θが、周期の途中段階を表すことに気付きました。
1周期、2周期目、3周期目・・・
と数えるだけじゃなくて、
1周期と角度πのところ、
2周期と角度π/4のところ・・・
と示せることに気づいた。
この余りの角度「π」「π/4」が位相。
周期の途中段階。
途中の様子。
それを、
数字で示せることに気づいた
んです。
つまり位相とは?
円を1周するまで(角度が2πに達するまで)の途中の段階。
英語ではフェーズと呼ばれるもの。
遊戯王をお知りなら、
たぶん理解は早いと思います。
位相は、
2πで1周期と定義したときの、
周回の余り。
ホニャララ周期と表記するには
余分な角度。
これが、
位相を表す値となるんですね。
周期のあまりだから、
0≦θ<2π
で決まる値です。
当たり前ですね。
位相とは、周期の「途中の角度」をいう。
およそ、
この理解で大丈夫です。
じゃあ結局、、「固定端反射は、位相が+π変わる」ってなんなのさ?
答えから言うと、
固定端反射は、位相が+π変わる
って、
周期が角度「+π」分進む
ってことですわな。

円1周分の角度で、1周期。
だから
2πで1周期と定義して、
固定端反射では、
その周期が「+π」分だけ進むってこと。
固定端反射した時、
その振動は
1周期の半分だけ進んだものに
変わるってこと。
周期と位相は対応してますから。
1周期=2π回転すること。
だから、
位相が「+π」変わる
↓
周期が「1/2周期」進む
ってことですね。
周期の1/2分、
運動の様子が変わるのです。
媒質の運動が、
グイッと捻じ曲げられる。
固定端に
振動が伝わった瞬間に。
跳ね返ってくる振動は、
周期の1/2分進んだものになる。
グルっと振動が反転して、
返ってくるわけです。
それが、固定端反射。
逆に、
自由端はそのままですね。
位相が変わらず、
つまりは
振動の様子が変化せずに
跳ね返ってくる。
自由端反射は、位相は変わらない。
固定端反射は、位相が+π変わる。
って、
そういう説明なのです。
お見知りおきを。