運動方程式を正しく立てられるなら解ける問題。それで完答可能ですな。 #東大2025 #第1問の問Ⅲ #力学 #質点3つ

 

（https://www.u-tokyo.ac.jp/content/400239120.pdf）

 

どうも、白滝です。

 

今回で東大力学の最後の問題。

 

（これまでの問題はこちら）

2次試験に向けて、東大2025年の物理でも解説しましょうか。#第1問の問Ⅰ #力学 #質点3つ

つり合いの式と最大静止摩擦力の公式と。#東大2025 #第1問の問Ⅱ #力学 #質点3つ

 

今回の問題は、

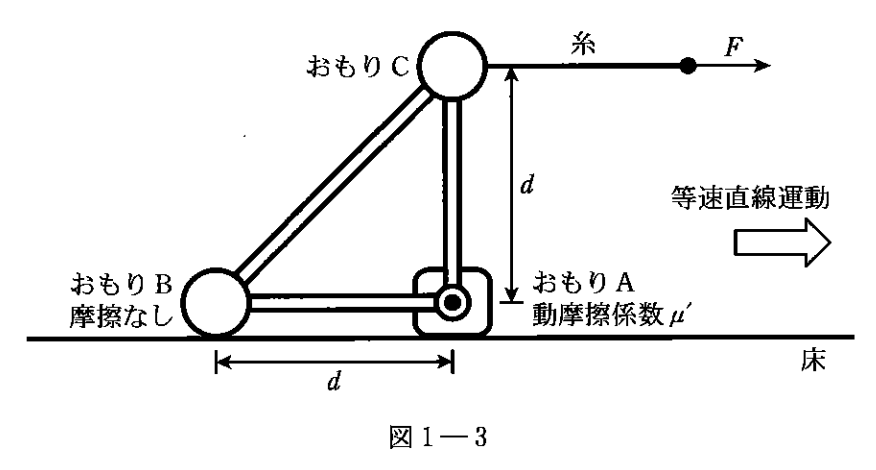
「おもりAとおもりBが床に接したまま」

というのがポイントですね。

 

たとえばもし、

 

おもりBが床から浮いて、

回転なんて始めてしまったら・・・

 

それは、ちょっと手間ですから。

（一応解けるが、回転する・しないの場合分けが必要）

 

今回の問題は、回転なんてしない。

 

それが前提の問題となりますぜ。

 

(1)はまたもや、力のつり合い。

 

等速直線運動しているということは、

加速度ゼロなので、

運動方程式$F=ma=m×0=0$

つまり、力がつり合っている状態ですね。（力の合力がゼロ）

 

よって、

$F=(おもりAの動摩擦力)$となる。

（全体での力のつり合い）

 

また、摩擦力の公式より、

$(おもりAの動摩擦力)=μ’N_{おもりA}$

 

また、前問より

$N_{おもりA}=2mg+F$とわかっているので、

この3式をFについて整理すると・・・

 

というのが、答えですね。

 

ええ。

 

エッセンスのままでしょう？

 

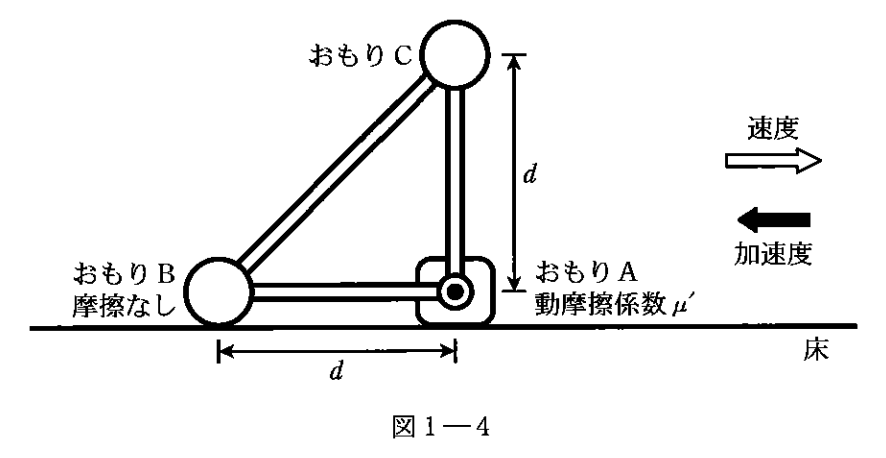
(2)は慣性力・・・でもいいが、運動方程式を立てればよし。

とりあえず、上下方向の力のつり合い（全体）で、

$(おもりABCによる重力)=(おもりAの垂直抗力)+(おもりBの垂直抗力)$

 

数式にすれば、

$3mg=N_{おもりA}+N_{おもりB}$

が成り立ちますね。

 

水平方向では等加速度を持つので、運動方程式が立てられます。

$ma=(おもりAの動摩擦力)$

 

また、摩擦力の公式より、

$(おもりAの動摩擦力)=μ’N_{おもりA}$

が成り立つ。

 

この3式を$N_{おもりB}$について整理すると、

与えられた値だけで$N_{おもりB}$が表現できますね。

 

ええ。

 

ただ、運動方程式を立てただけ。

 

別に慣性力を設定してもいいですが、

【最強解説】慣性力がわからなすぎてエグい人へ。

 

今回はシンプルな話なので、

運動方程式を立てるだけ。

 

そんな大したこと、してないですわ。w

 

(3)は慣性力+モーメントの融合問題。

 

そう。

 

式が1本足りないのです。

 

$a$を求めるには。

 

式があと1つ足りない。。

 

だから、この等加速度運動の中で、モーメントを計算する必要があります。

 

さすが、東大。

 

その力学の最終問題。

 

さすがに、応用を効かせてきましたな。

（でも、解けずとも約89%は得点できている）

 

そう。

 

解けなくてもいい。

 

捨ててもいい。

 

でも、まあ、

解こうと思えば解けるので。

 

（解ける人は、こちらでも解いてみてくださいな）

 

または(3)は、運動方程式だけでも解けるんだわな。w

もう1本、式が欲しい。

 

(2)で$N_{おもりB}$を$a$の式で表したから、

もう1本、$N_{おもりB}$と$a$の式が欲しい。

 

・・・ですよね？

 

だから、

おもりBとおもりCそれぞれで、運動方程式を立てればいい。

 

それだけです。

 

ええ。

 

(2)では全体で運動方程式を立てたので、

もっと式が欲しいなら、

個別で式を立ててあげればいい。

 

とくに、今回ほしいのは、

$N_{おもりB}$と$a$の式

なので。

 

狙いどころは、限られるわけですな。

（狙いをつけなくても、全部のおもりについて、上下左右の運動方程式を立ててから考えても解けまっせw）

 

そう。

 

んで、今回まずわかりやすいのは、

おもりBの$N_{おもりB}$ですよね。

 

これは、おもりBについて、

上下方向の運動方程式（静止しているので、つり合いの式）を立ててあげれば、取り出せますわな？

 

$N_{おもりB}=mg+T cos45°$

（$T$は斜めの棒から受ける力）

 

んで、この$T$はおもりCにもかかるので、

おもりCについて、水平方向に運動方程式を立てると、

 

$ma=T cos45°$

 

よって、この2式から、

$N_{おもりB}=mg+ma=m(g+a)$

 

これで、

$N_{おもりB}$と$a$の式

が得られたので、

 

あとは(2)の答えと連立して計算すれば・・・

答えが出るわけですな。

 

ただ、正しく運動方程式を立てただけ。

これで解けるのが、東大です。

 

たとえ最短ルートがわからなくても、

全ての物体についてとりあえず運動方程式を立てて、

あとはゴリゴリ計算すれば解けますので。w

 

マジで。

 

そんな大きな時間ロスなく、

大問の1つを完答できる。

 

やることは、正しく運動方程式を立てること。

 

加速度がゼロなら、

それは勝手につり合いの式になるだけなので。

 

正しく、力の作図をする。

 

正しく、$ma=F$に代入する。

 

じゃあ、その正しいとはなにか。

 

!00%確実に運動方程式を立てるには、

どうすればよいか。

 

もしご興味があれば

 

↓

↓

 

⇒迷わないための、マニュアル。