(https://www.dnc.ac.jp/albums/abm.php?d=771&f=abm00005964.pdf&n=2025_op_39_butsuri.pdf)
振幅とは?
単振動とは?
これを数式化すると、なんなのか知っていますか?
というのが、今回の問題。
え
知ってました?
ーーーーーーーー
【今回使う知識】
- 単振動する物体の運動:$sinθ、cosθ$で表される。(周期関数)
- 単振動する物体の最大位置、最小位置(の絶対値):これを振幅という。
- $sinθ、cosθ$の位相の知識
ーーーーーーーー
すみません、この説明を読むにも、
周期関数とはなにか?絶対値とはなにか?という知識が必要で。
(数学の知識ですねw)
位相の知識も必要ですね。(まあ、今回は三角関数(単位円)の知識があれば、解ける。)
そう、要は知識なのです。
普通に、ただ教科書にある知識が問われている。
んで、今回は、
振幅と単振動の話。
その知識があるか、を問うているのですね。
↓
↓
(Gemini3の解答)
解説
1. 空欄 [ア]:変位 $s$ を表す式
問題文の条件を確認します。
-
振幅:$L\theta_0$
-
時刻 $t=0$ の状態:点O(変位 $s=0$)を、負から正の向きに通過した。
この運動をグラフにすると、原点($0,0$)からスタートして右上がり(正の方向)に進む波形になります。
-
$\cos \omega t$ の場合:$t=0$ で $s = L\theta_0$(最大値)となるため不適です。
-
$\sin \omega t$ の場合:$t=0$ で $s = 0$ となり、その後の傾き(速度)も正なので条件に合致します。
よって、[ア] には $\sin \omega t$ が入ります。
2. 空欄 [イ]:角振動数 $\omega$
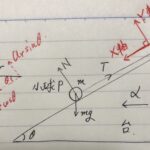
単振り子の運動方程式から導きます(または公式として覚えているものを適用します)。
問1の結果より、復元力 $F$ は以下のように近似されました。
変位 $s$ と角度 $\theta$ の関係は $s = L\theta$ なので、$\theta = \frac{s}{L}$ を代入します。
これを運動方程式 $ma = F$ に代入すると、
単振動の加速度の公式は $a = -\omega^2 s$ です。これと比較すると、
よって、[イ] には $\sqrt{\frac{g}{L}}$ が入ります。
結論
-
[ア]: $\sin \omega t$
-
[イ]: $\sqrt{\frac{g}{L}}$
この組み合わせを選択肢から探すと、① が正解となります。
正解: ①