どうも、白滝です。
どうでしょう?
勉強は順調に
進んでおりますでしょうか?
今回は、
縦波(たてなみ)
という
波動のはてなポイントに
立ち向かって
いきたいと思います。
こいつですね。
コレ。
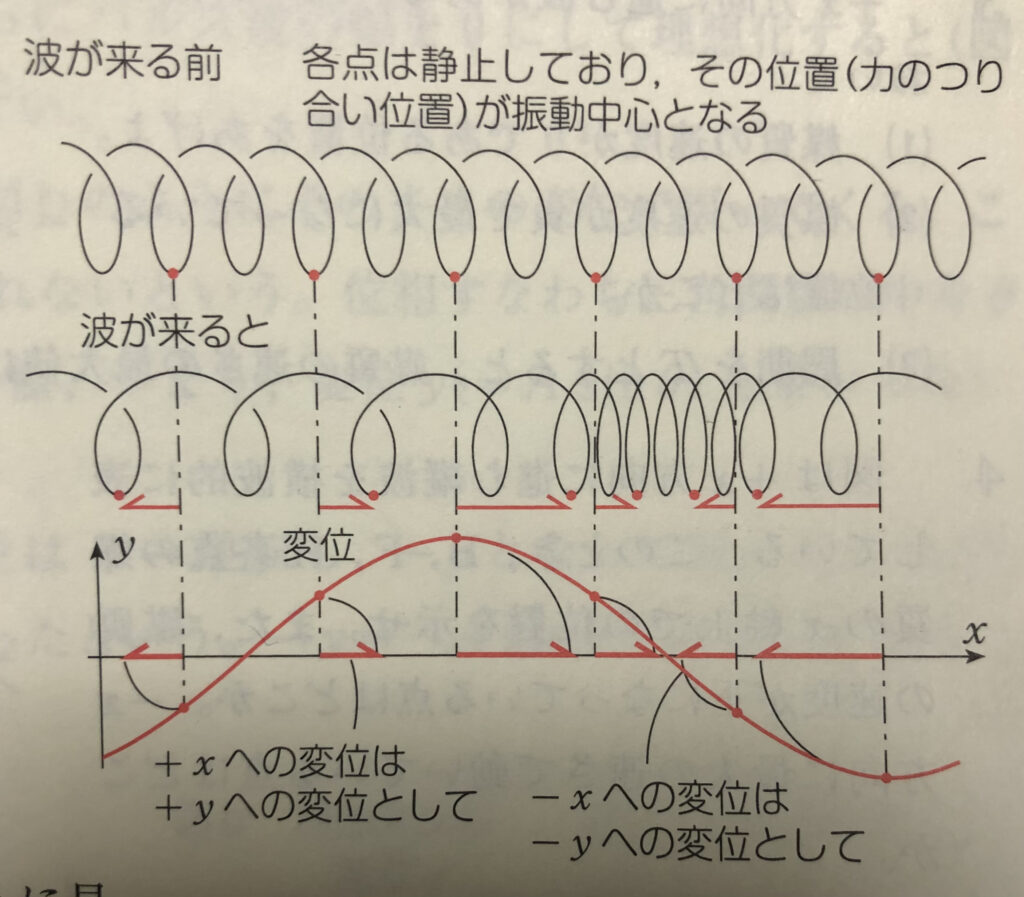
(物理のエッセンスより引用)
縦波ってここに
書いてある通りなのですが、
かなーり難しい。
バネが振動して、
その各点の変位をy軸にとって、
x軸には・・・
って。
図で解説してくれては
いるんですが・・・
結局、なにしてるの?
と思いませんか?
横波→現実の波をそのままグラフ化したもの!
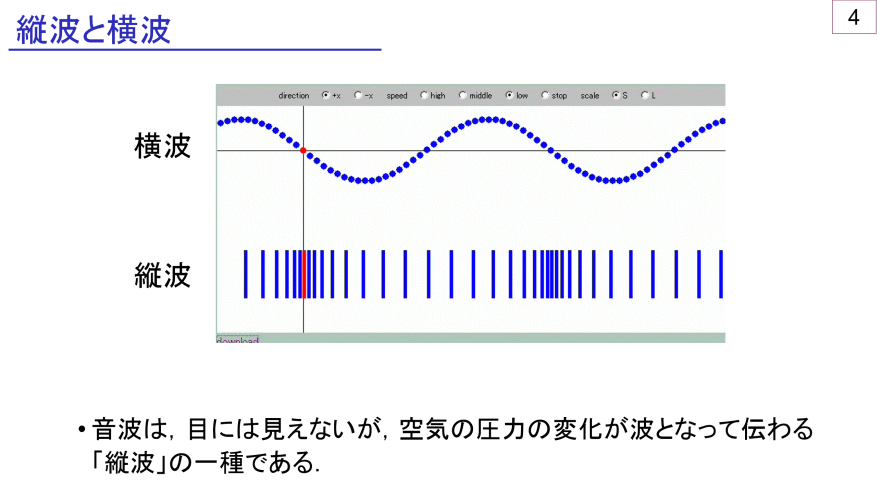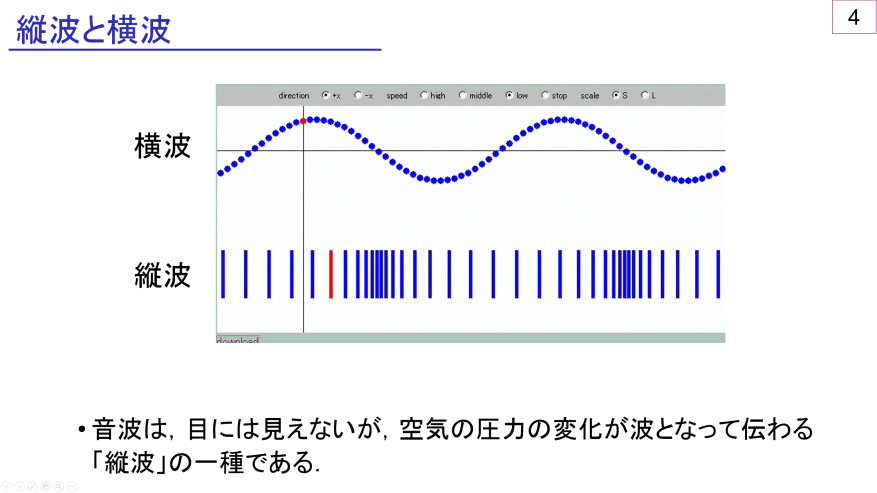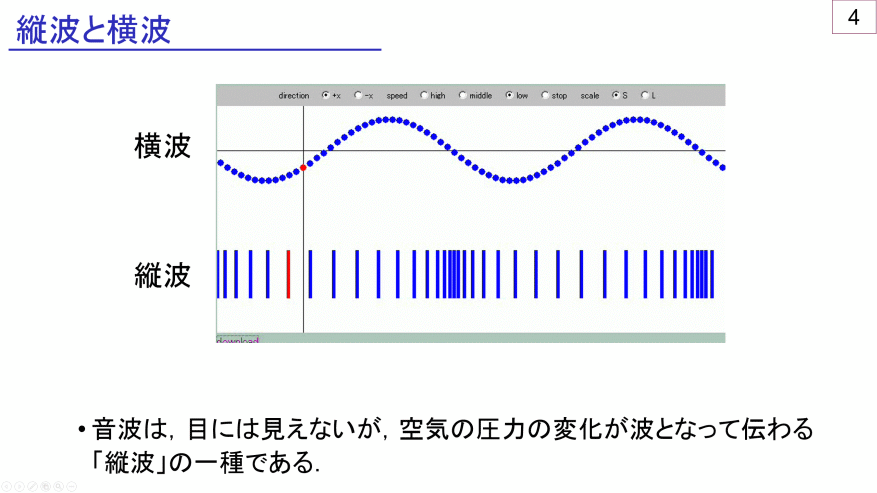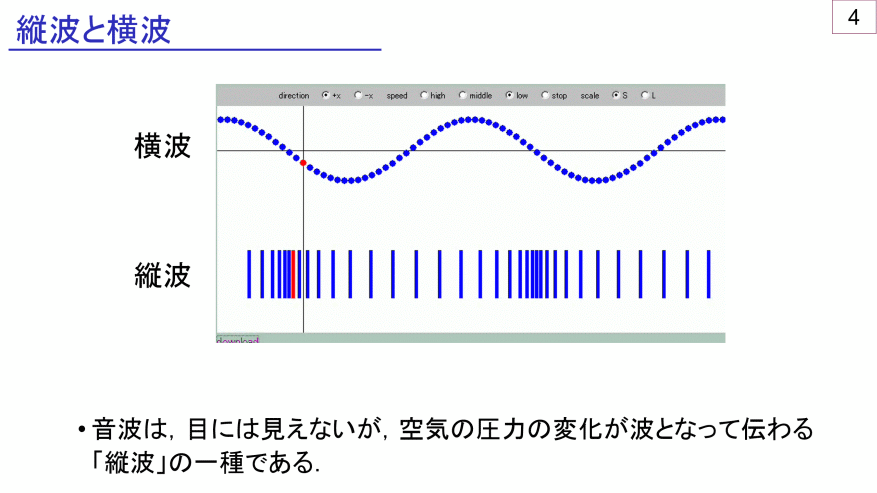
縦波→現実では「波の形」をしてないもの!
(だから、定義をつくって無理やりグラフ化した)
横波と縦波の違いは、これでしたね。
縦波は
現実では「波の形」をしていないから、
定義をしないと
グラフ化できなかった。
現実では、水の波紋のようにザッブーンと「波の形」があるわけではなく、
バネの揺れだったり、
空気の振動だったり・・・
と媒質が振動しているだけ。
でも、
物理学者は思った。
横波と同じように、縦波もグラフ化できるんじゃね?
y→自然な位置からのズレ。
x→自然な時(振動してない時)の点の位置。
これです。
これが、
縦波をグラフ化するための定義。
縦波はムズカシイ定義をすることによって、グラフ化されています。
だから・・・
縦波で難しいのって、
「現実の波の様子←→グラフの形」
の変換なんですわ。
縦波自体じゃなくて。
縦波をグラフに変換するために使われている、定義がムズい。
これね。
y→自然な位置からのズレ。
x→自然な時(振動してない時)の点の位置。

この定義通りにバネの各点を、
y-xグラフ
にプロットしてあげると、波のグラフが完成するんだけど・・・
おそらく、
あなたはこの定義が
意味不明だから行き詰まっている。
この定義のせいで、
縦波に苦手意識をもっているのでは?
リアル振動の様子から、グラフへの変換。
または、
グラフから、
リアルの振動の様子を想像すること。
ここが難しい。
逆に言えば、難しいのはココだけなのです。
「現実の波の様子←→グラフの形」の変換が難しいだけで、
ほかは横波と同じですよ?
グラフ化してしまえば。
周期の計算も。
波長の読み取りも。
その先はみーんな、同じこと。
ちょっとグラフから、
縦波の疎と密
が読み取れるだけで、
ほかはみーんな同じ。
「現実の波の様子←→グラフの形」の変換以外は、意外とカンタンなのが縦波なのですわ。
じゃあ、、「現実の波の様子←→グラフの形」の変換ってどうやるの?
なんども言いますが、これです。
y→自然な位置からのズレ。
x→自然な時(振動してない時)の点の位置。

この定義通りにバネの各点を、
グラフに変換してあげる。
または、
グラフからバネの各点の位置を
読み取ってあげる。
そのほかはフツーの波と同じ。
同じなのですね。








