問題演習お疲れ様です。
ここからの解答は、
ルールに従って解くこと
を大事にしてます。
どんな問題でも、
確実に解くために。
この目の前の
問題を解けたところで、
入試問題を解けなかったら
意味ないですから。
ルールを身に付ける。
さすれば、
どんな問題でも簡単に解けます。
同じ作業です。
【物理のエッセンス(力学)問23(b)】
合成ばね定数$k_T$を求めよ。
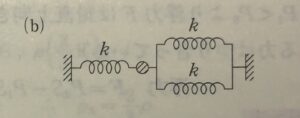
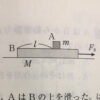
両端に壁がある問題。
これも(a)と同じく難問ですね。
力の作図をするにしても、
そもそも、どれに注目したら良いかわからない!
ってなりますな。
バネは両側の壁に押されていたり、引っ張られていたり・・・
正常じゃないわけです。
じゃあ、
どうやって運動方程式(つり合いの式)を立てていくのか?
注目する物体
が大事になります。
ちょっとした特殊例ですね。
⓪問題文をちゃんと読む。
:与えられた条件、 : 求めるもの。
【物理のエッセンス(力学)問23(b)】
合成ばね定数$k_T$を求めよ。

①注目する物体を1つに決める。
少し難しいが、「3個のバネをひとカタマリにした全体」に決める。
②その物体に働く力を図示する。

物体同士が接触している。
→必ず、摩擦力と垂直抗力が発生している!
【これが例外なだけ】
床が「なめらか」→摩擦力は0。
壁が「なめらか」→摩擦力は0。
物体の表面は「なめらか」
→摩擦力は0。
カベ(左右とも)はバネと接しているから、$F_1,F_2$を書き込む。
垂直抗力の「くっ付いてる」バージョン。
→押し合うだけでなく、「引っ張り合う」場合があある。
→垂直抗力は$0$になると離れるが、くっ付いてると「押し合う→$0$→引っ張り合う」
これには名前はないんだね。
向き→接地面の垂直方向。垂直抗力は「押し合う」方向だが、くっ付いているのでどちらでも良い。(計算結果がマイナスなら設定した向きと逆向き、プラスなら設定した向きが正しい向き)
(今回は摩擦力なし)
③$x$軸と$y$軸を設定する。(または$x$軸だけ)
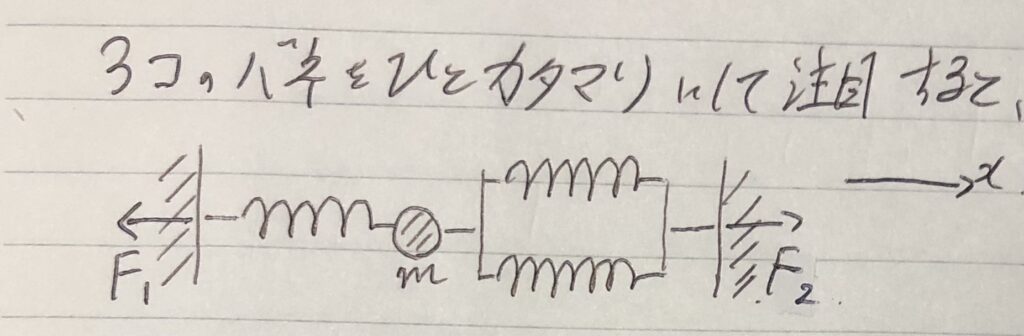
水平右向きを正とする。
④力を分解する。
今回はなし。
⑤$x$軸方向と$y$軸方向それぞれで、運動方程式「$ma=F$」に代入する。
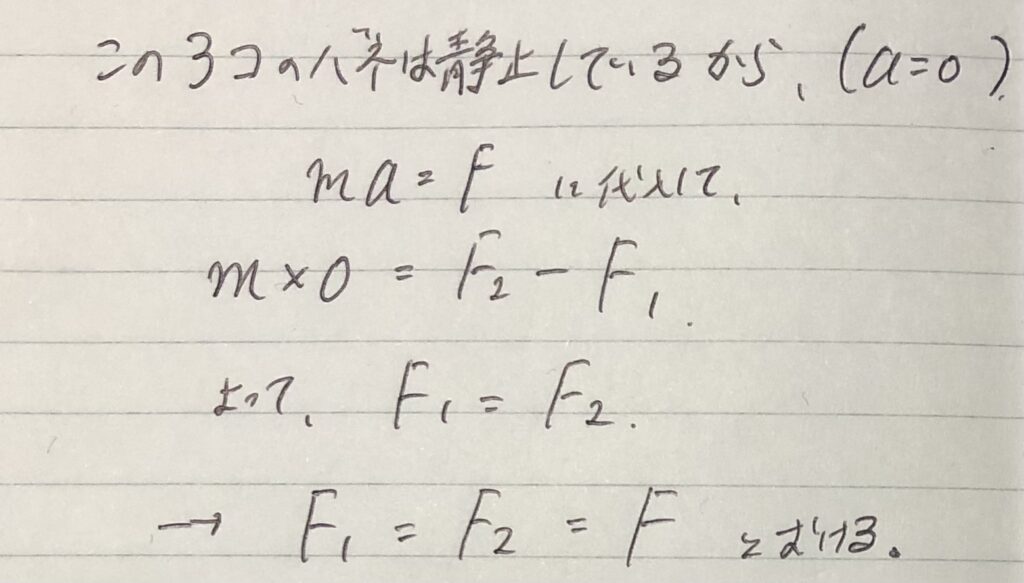
⑥作用・反作用の法則の等式を立てる。($N=N’$とか、$f=f’$とか。)

【両側にカベがある問題】
→カベとの作用・反作用を考える。
まず始めに「壁に挟まれた全体」を両側のカベが力$F$で引っ張っている、と考える。
次に「そのカベとの作用・反作用」から力の等式を立てる。
両側をカベで挟まれた問題は、かなり特殊な問題。
カベが「内側の全体」を力 $F$で引っ張っていること、「そのカベとの作用・反作用」で力の等式が立てれることを使う必要がある。

⑨式を計算する。

ここまでが物理。
ここからは数学のハナシ。
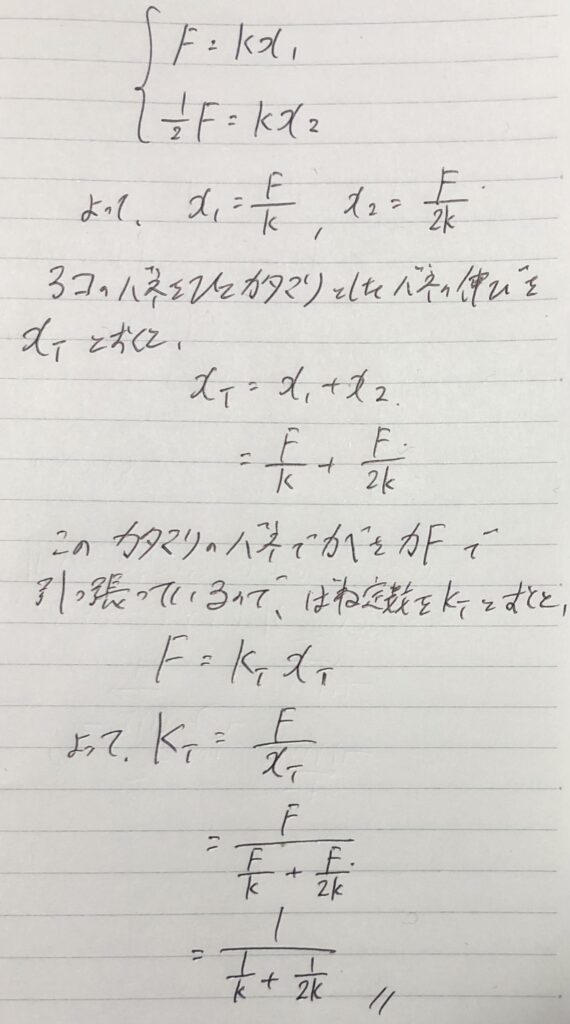
うーん。。
難しいですな。
壁に挟まれている
→中の物体をひとくくりに「注目物体」として設定する
→それにはたらく力を作図する
ってのが攻略法ですわ。
以上です!
問題24以降も
同じように解いていくので、
よろしく。