問題演習お疲れ様です。
ここからの解答は、
ルールに従って解くこと
を大事にしてます。
どんな問題でも、
確実に解くために。
この目の前の
問題を解けたところで、
入試問題を解けなかったら
意味ないですから。
ルールを身に付ける。
さすれば、
どんな問題でも簡単に解けます。
同じ作業です。
【物理のエッセンス(力学)問40】
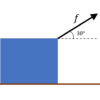
動摩擦係数$μ$の床上にある質量$m$の物体に、(水平右向きから)$30°$の向きに力$F_0$を加え続けてすべらせた。加速度を求めよ。
(物体は床から浮かないものとする)
⓪問題文をちゃんと読む。
:与えられた条件、 : 求めるもの。
【物理のエッセンス(力学)問40】
動摩擦係数$μ$の床上にある質量$m$の物体に、(水平右向きから)$30°$の向きに力$F_0$を加え続けてすべらせた。加速度を求めよ。
(物体は床から浮かないものとする)
①注目する物体を1つに決める。
もちろん、「物体」に決める。
②その物体に働く力を図示する。
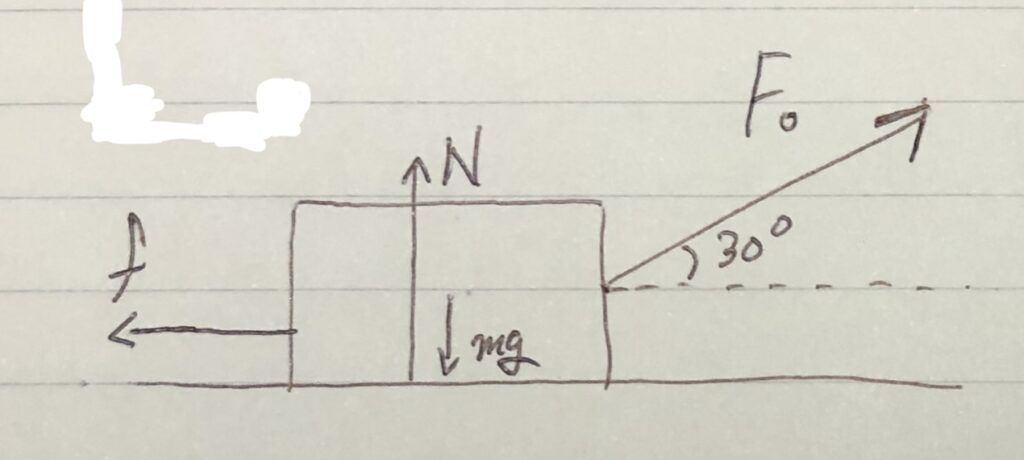
問題文から→$F_0$
質量$m$をもつ→重力$mg$がかかる。
また、
物体同士が接触している。
→必ず、摩擦力と垂直抗力が発生している!
【これが例外なだけ】
床が「なめらか」→摩擦力は0。
壁が「なめらか」→摩擦力は0。
物体の表面は「なめらか」
→摩擦力は0。
物体は床と接しているから、
摩擦力$f$と垂直抗力$N$を書き込む。
③$x$軸と$y$軸を設定する。(または$x$軸だけ)

④力を分解する。
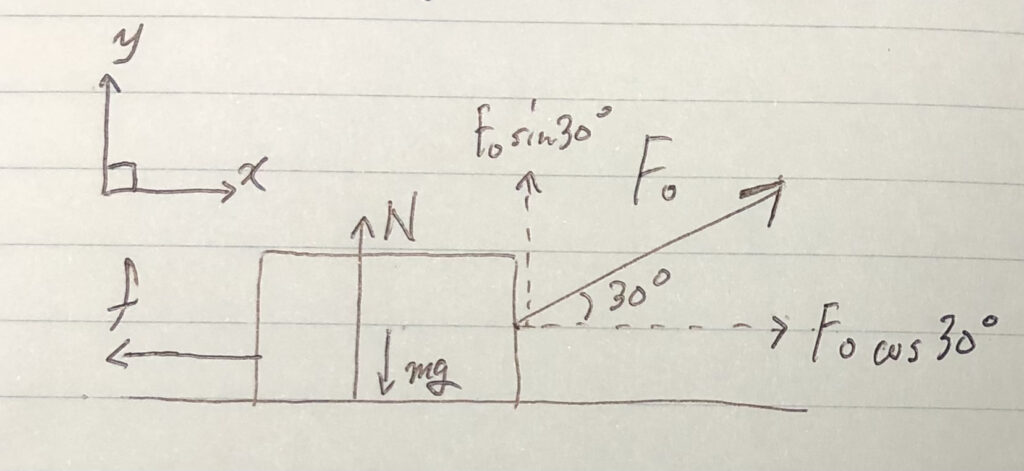
$F_0$を$x$軸方向と$y$軸方向に分解する。
⑤$x$軸方向と$y$軸方向それぞれで、運動方程式「$ma=F$」に代入する。
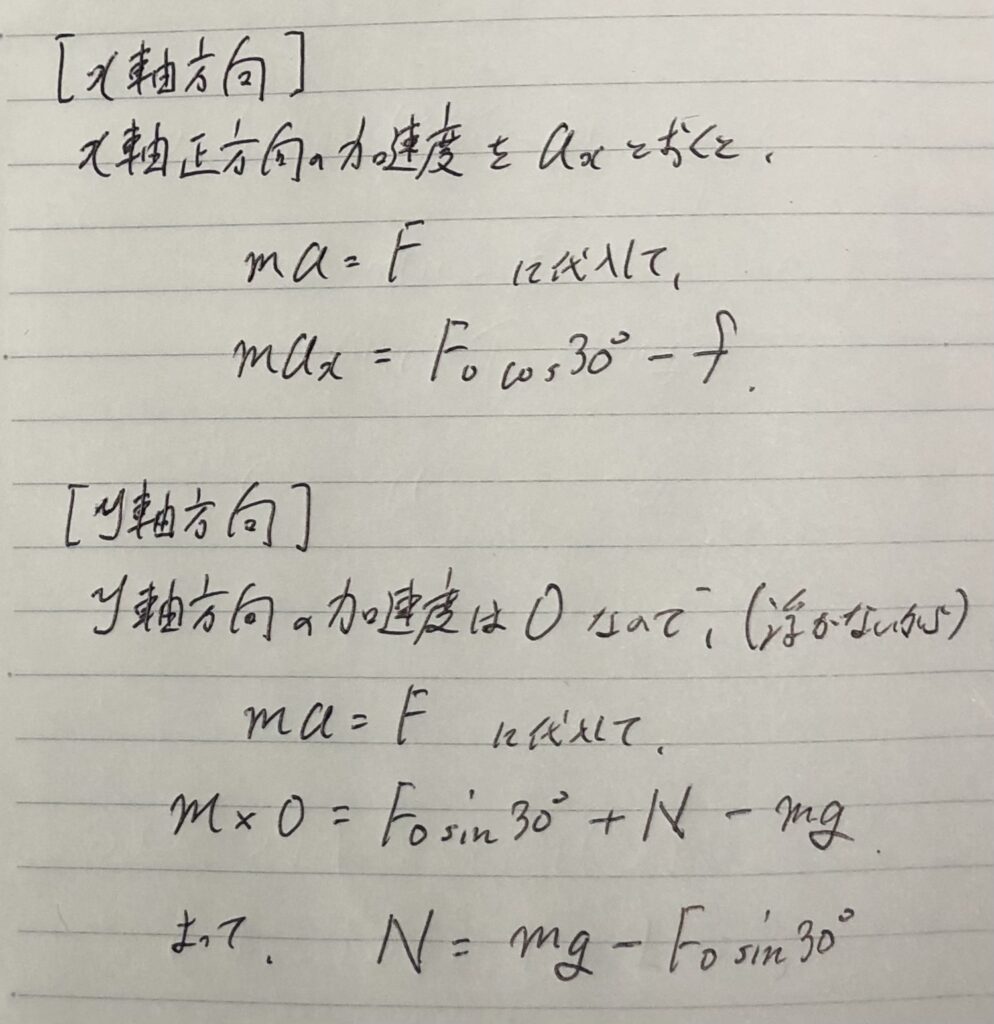
⑧作用・反作用の法則の等式を立てる。($N=N’$とか、$f=f’$とか。)
今回はなし。
⑨式を計算する。
【摩擦力の扱い方】
①滑っている時→動摩擦力 $μ’N$
②静止している時
- 単なる静止なら
→fとおいて力のつり合いで求める。
- まさに動くギリギリなら
→最大(静止)摩擦力 $μ’N$
これを使って、


物体が上に引き上げられる→垂直抗力$N$が減る→動摩擦力$f=μN$が小さくなる
という問題。
だから、物体の加速度はこんなオカシナ値になっている。
テキトーに解く学生には、超難問。
物理がキライになる問題やね。w
でも、
ルール通りに解けば、当たり前のように答えが出る。
物理はロジカルだから。
ルールを守れば、答えは出るのだ。
以上です!
問題41以降も
同じように解いていくので、
よろしく。