目次
物理の問題の解き方3ステップ。(復習)
1.目の前で起こっている現象を「把握」する。
→力の作図をして、図に書き出す。
2。公式に当てはめて、方程式をたてる。
→力なら、運動方程式(F=ma)に当てはめるだけ。
3.方程式を計算する。
物理の問題はすべて、この3ステップで解いていきます。
そのためには、まず、
はたらいている力を図に「正しく」記入することが必要です。
力の作図については、前回に解説しましたね。
今回は2番目、
「公式に当てはめて、方程式をたてる。」
を解説していきます。
方程式を立てる前に、自分でX軸とY軸を設定する。
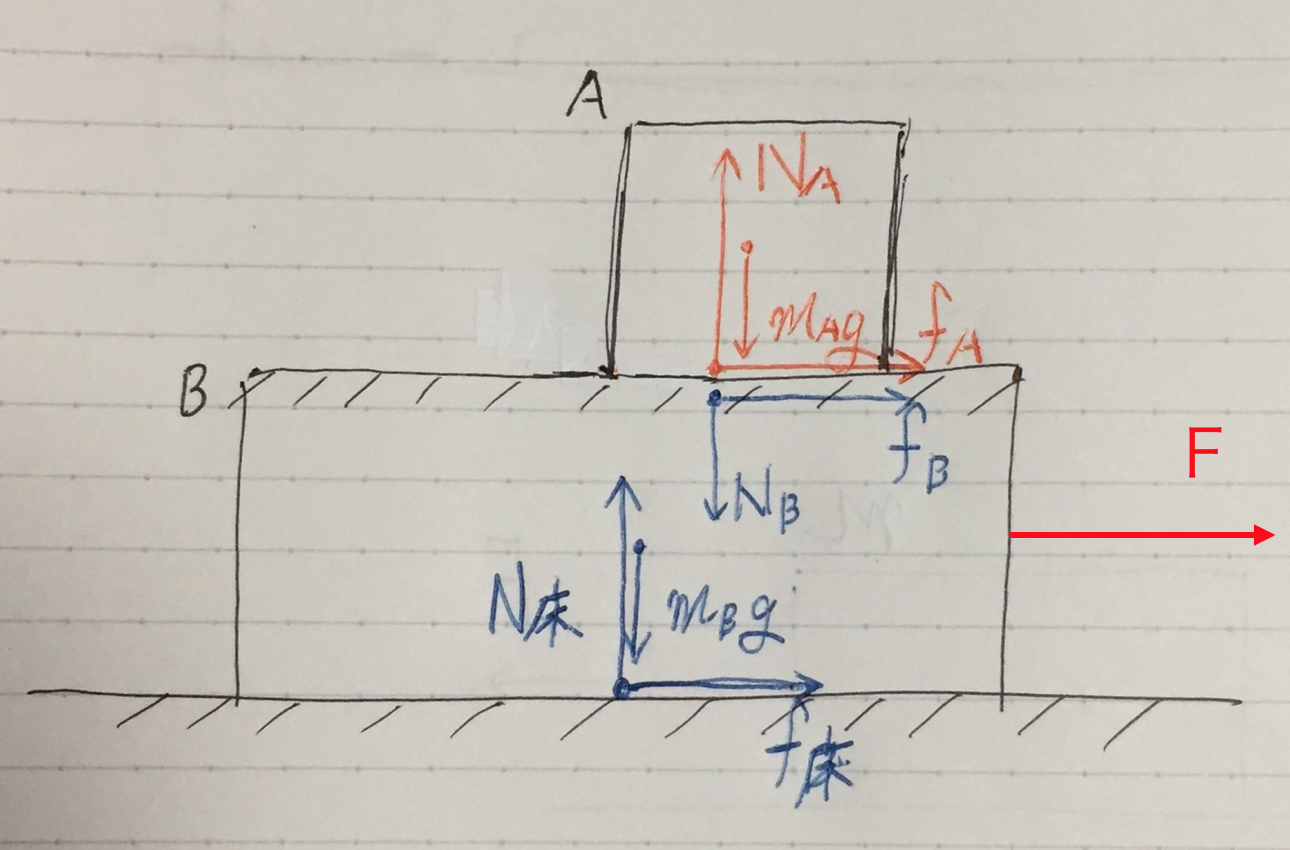
力の作図は前回、完成させましたね。
ここから方程式をたてるには、
自分でX軸とY軸を設定しないといけないんです。
ルールその1.
自分でX軸とY軸を設定する。
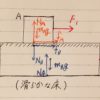
今回は、
・右方向をX軸の正方向
・鉛直上向きをY軸の正方向
に設定してみました。
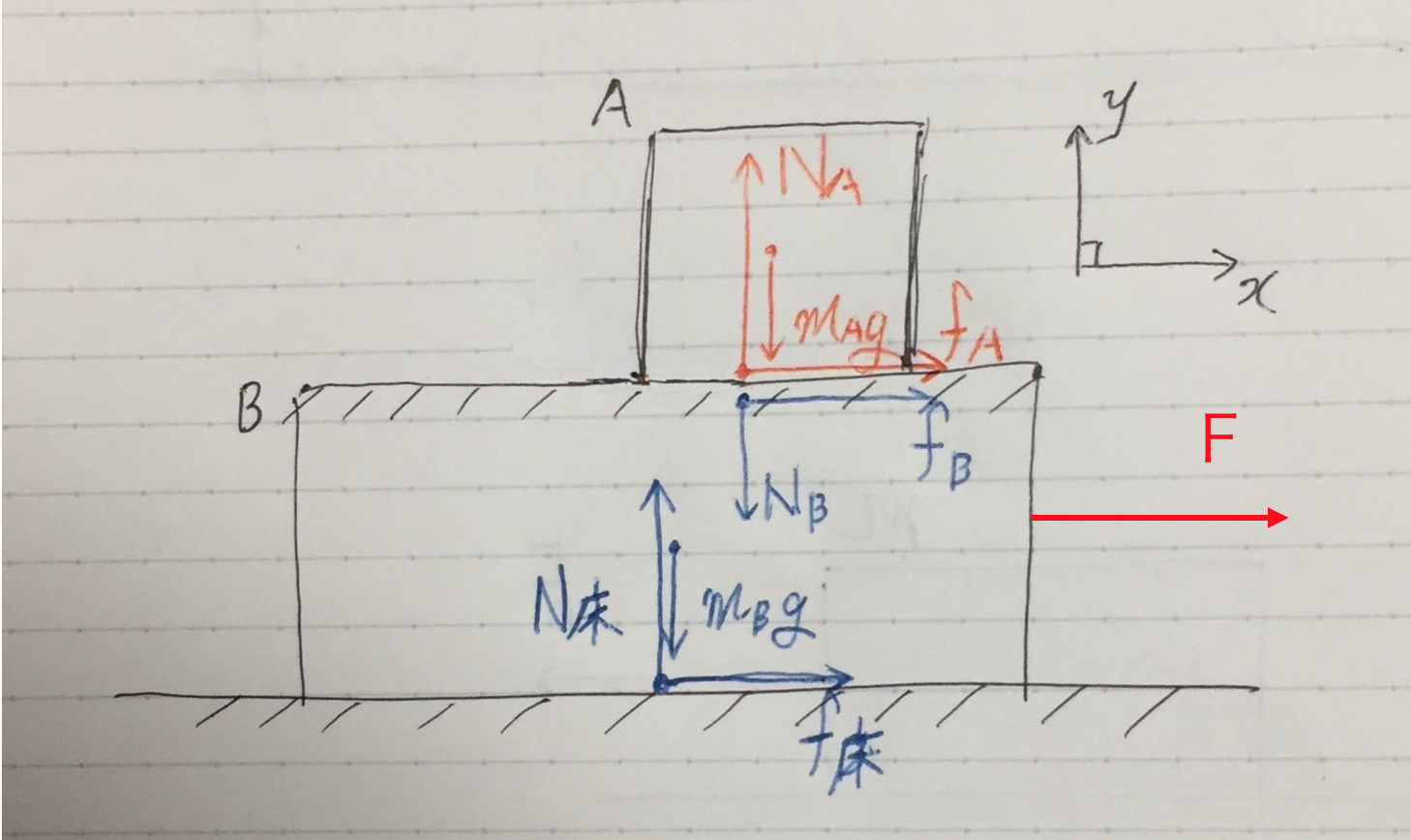
X軸とY軸を設定することで、
・X軸方向の運動方程式
・Y軸方向の運動方程式
の2つの式が立てられるようになります。
つまり、この2つの式を順番に立てていけば、方程式は完成するんです。
運動方程式は、物体1つにつき、2つ立てる。
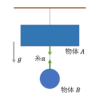
今回は物体Aと物体Bがあるので、
・物体AのX軸方向の運動方程式
・物体AのY軸方向の運動方程式
・物体BのX軸方向の運動方程式
・物体BのY軸方向の運動方程式
の4つの式が立てられるわけですね。
式を立てるときは、運動方程式ma=Fに代入するだけです。
具体的には、
m(質量)には、その物体の質量。
a(加速度)には、その物体の加速度。(わからないときは文字のままで)
F(力)には、その物体が受ける力。(矢印の向きが正方向の力はプラス、矢印の向きが負の方向の力はマイナス)
で代入してください。
このルール通りに運動方程式を立てると、
・物体AのX軸方向の運動方程式

ma=F に、
m(質量)には、物体Aの質量mA。
a(加速度)には、物体Aの加速度aA。(わからないときは文字のままで)
F(力)には、物体AがX軸方向に受ける力fA。(矢印の向きが正方向の力はプラス、矢印の向きが負の方向の力はマイナス)
を代入しました。
これがわからない人は、力の作図と見比べて「なにをどう代入しているのか」掴んでみてください。

はっきり言って、「式の立て方=公式に代入するだけ」です。
では、残りの運動方程式も立てていきましょうか。
・物体AのY軸方向の運動方程式
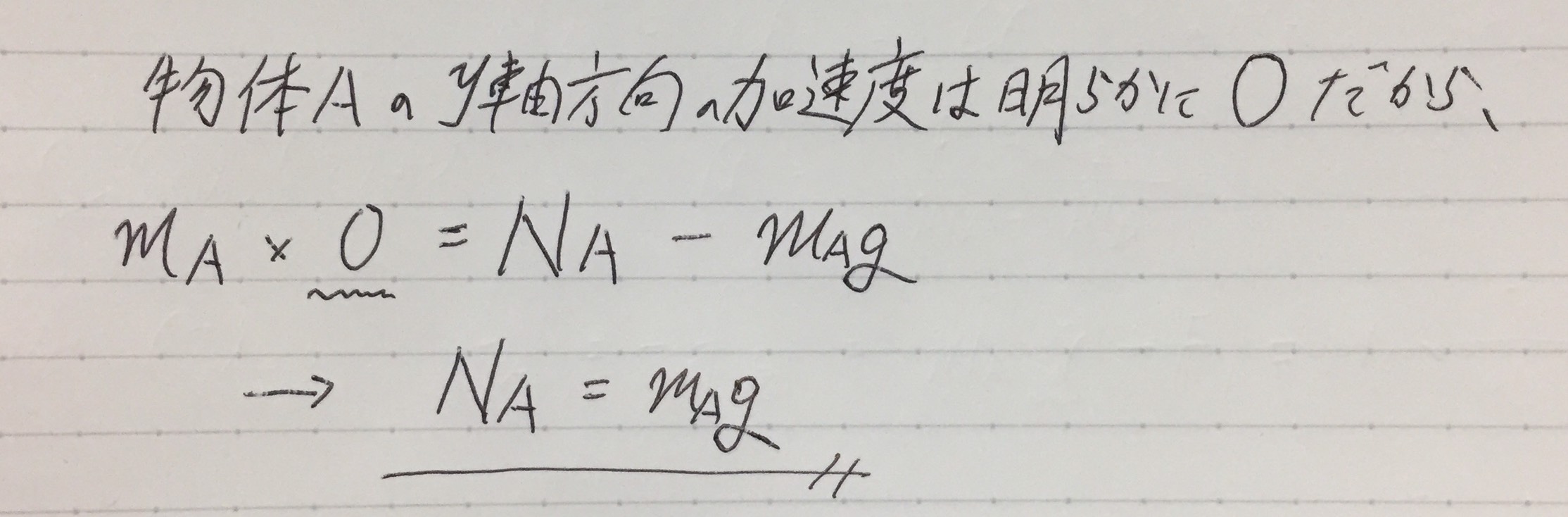
ma=F に、
m(質量)には、物体Aの質量mA。
a(加速度)には、物体Aの加速度0。
F(力)には、物体AがY軸方向に受ける力『NA-mAg』。(矢印の向きが正方向の力はプラス、矢印の向きが負の方向の力はマイナス)
を代入しました。
加速度が0のときの運動方程式を、特別に「力のつりあいの式」と呼びます。
NA=mAgって、つりあいの式でも立てられるんですが、
運動方程式でも問題なく式を立てられるんです。
もちろん、ここはつりあいの式で立ててもOKですよ。
(私はすべて運動方程式で立てる派です)
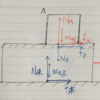
・物体BのX軸方向の運動方程式
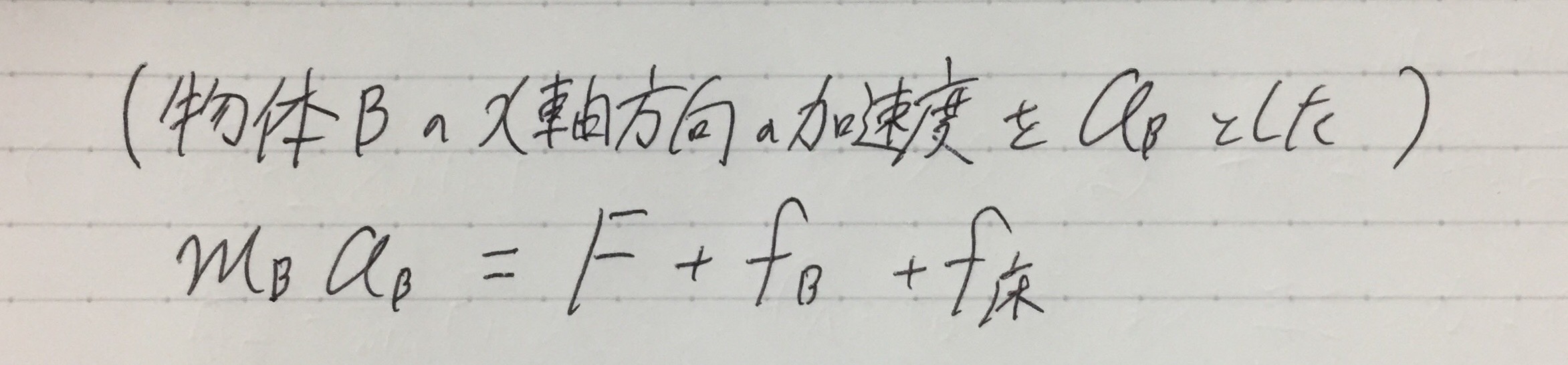
ma=F に、
m(質量)には、物体Bの質量mB。
a(加速度)には、物体Bの加速度aB。(わからないときは文字のままで)
F(力)には、物体BがX軸方向に受ける力『F+fB+f床』(矢印の向きが正方向の力はプラス、矢印の向きが負の方向の力はマイナス)
を代入しました。
・物体BのY軸方向の運動方程式
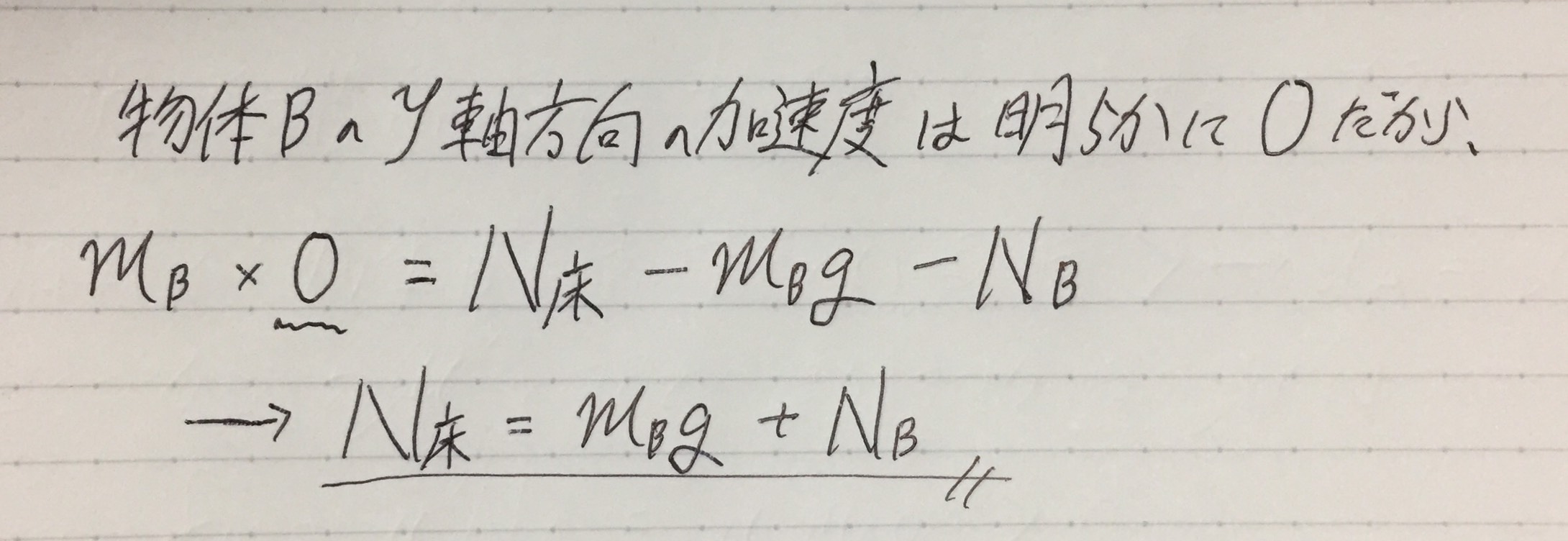
ma=F に、
m(質量)には、物体Bの質量mB。
a(加速度)には、物体Bの加速度0。
F(力)には、物体BがY軸方向に受ける力『N床-mBg-NB』(矢印の向きが正方向の力はプラス、矢印の向きが負の方向の力はマイナス)
を代入しました。
これも、つりあいの式でもOKです。
式の立て方=公式に代入するだけ。
運動方程式を立てるまでに、
直感も物理的センスも1つも要りませんでしたね。
ルール通りに、1個ずつ、値を代入していっただけでした。
m(質量)には、その物体の質量。
a(加速度)には、その物体の加速度。(わからないときは文字のままで)
F(力)には、その物体が受ける力を。(矢印の向きが正方向の力はプラス、矢印の向きが負の方向の力はマイナス)
ただただ、ルール通りに代入してください。
料理するときと同じです。
レシピに書いてある通りに料理すれば、だれだって美味しい料理が作れます。
なので、物理の問題演習というのは、
「ただただルール通りに計算できるか」の練習なんです。
どの問題を解いていても、やることは一緒です。
ルール通りに、決められた手順で問題を解くこと。
その手順がわからないなら、もう一度最初から、じっくりと読んでみてください。
わかるまで読んで、わかったら自分で手を動かして、式を立ててみてください。
運動方程式を立てられるかどうか、が物理の第一関門です。
運動方程式を立てられれば、力学の問題はおおよそ解けます。
物理が、入試の得点源になる・・・のはそのあたりからですね。
どうか、運動方程式を立てられるようになってください。
そのための手順は、ここにすべて公開しました。
あ、あとはおまけです。
「3.方程式を計算する。」が残っているんですが・・・ぶっちゃけおまけです。
運動方程式が立てられれば、99%の仕事は終わりだからです。
まあ、気になる方向けに・・・

この物体A,Bの加速度を求めてみましょうか。
いまわかっているのは、この4式ですね。
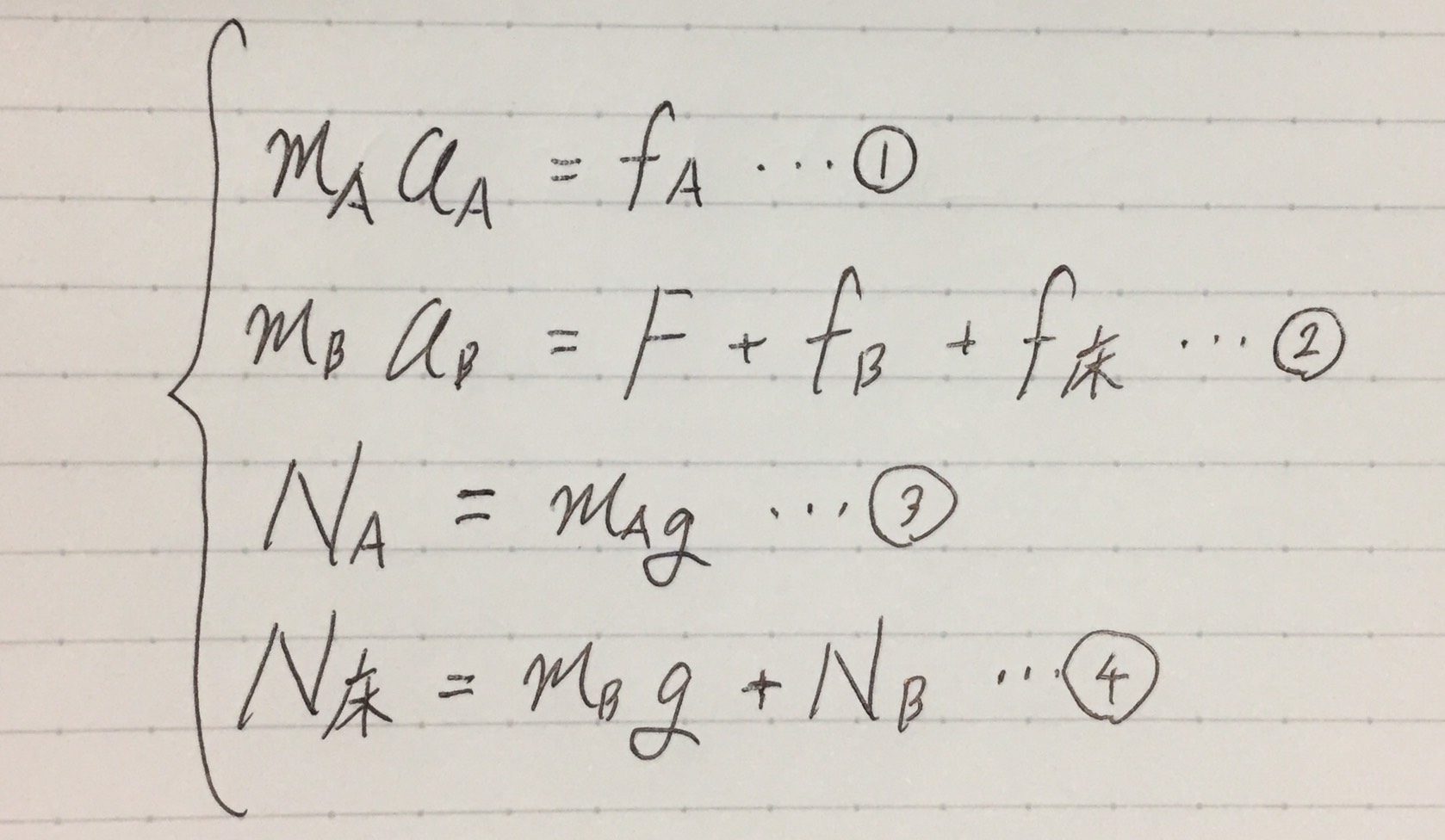
これに加えて、
物体A,Bの間の作用反作用の法則より、

が成り立ちます。
あとは、摩擦力の式があります。
物体が静止しているとき→fと置いたまま。
物体が動いているとき→f=μN の公式が使える。
というのが、摩擦力の式でした。
なので、
物体が静止しているときと、
物体が動いているときで場合分けしないといけません。
(数学では、基本的な考え方ですね)
よって、今回は、
・物体Aが物体Bの上を滑っていない場合
・物体Aが物体Bの上を滑っている場合
の2つの場合を考えていきます。
(物体Aと物体Bの間の動摩擦係数をμAB、物体Bと床の間の動摩擦係数をμB床とします。)
ここからは、数学の範囲です。
<物体Aが物体Bの上を滑っていない場合>
→物体Aと物体Bが一体になって動いている。
→物体Aと物体Bの加速度が同じ。
→つまり、aA=aB だから、これをaA=aB=aと置くと、
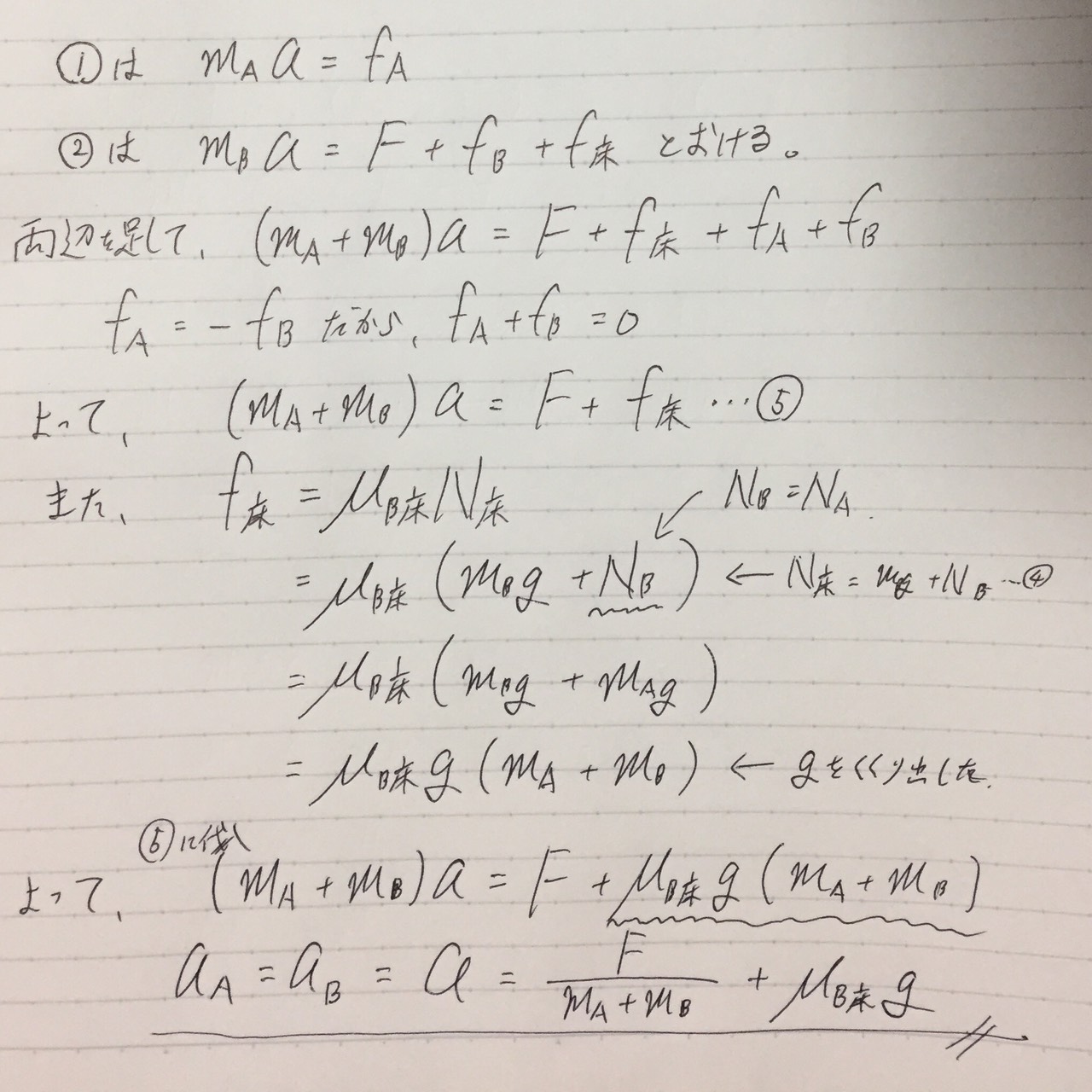
と、解けましたね。
(難しく見えますが、ただの式変形です)
<物体Aが物体Bの上を滑っている場合>

これで、aAは求まりました。
残りのaBは、
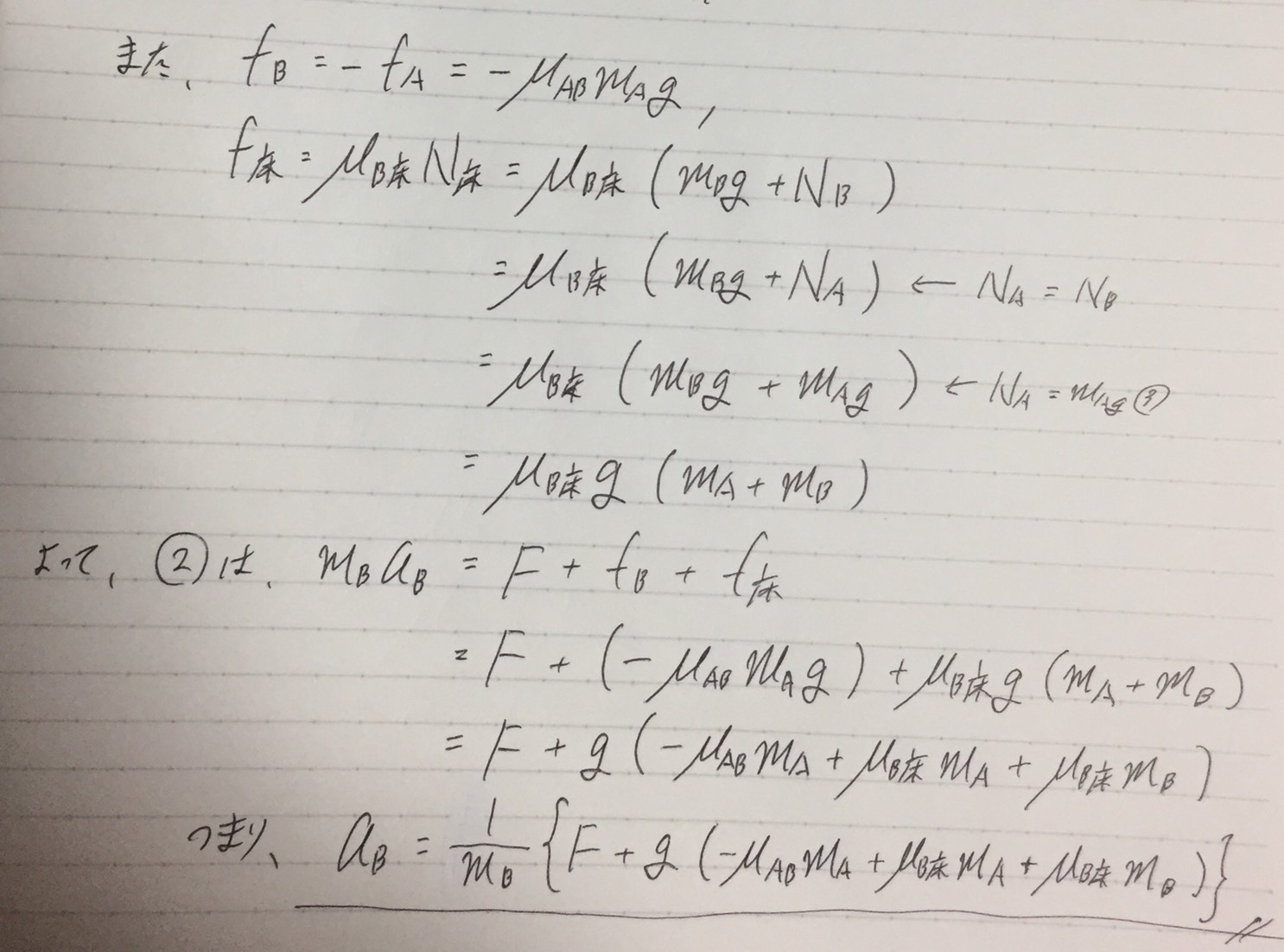
こんなかんじで、ひたすらに式を整理していくだけです。
(やはり物理というよりも、数学の範囲ですね)
物理が関係するのは、式を立てるところまでです。
作用・反作用の法則と、摩擦力の式が立てられれば、
その先は「数学」の話になってきます。
立てた式を組み合わせて、連立方程式を解くだけですね。
文字の計算になっただけで、いうて中学校の範囲です。
ここが苦手という方は、なんども計算練習していきましょう。
物理センスではなくて、計算練習の話です。
漢字ドリルで漢字の書き取り練習をするように、
なんどもやっていたら慣れます。
だって、中学校でやっていたことを「文字で」やっているだけですから。
わかりますか?
物理の計算ができないって、ただ計算練習が足りないだけなんです。
1.目の前で起こっている現象を「把握」する。
→力の作図をして、図に書き出す。
2。公式に当てはめて、方程式をたてる。
→力なら、運動方程式(F=ma)に当てはめるだけ。
3.方程式を計算する。
たった、3ステップです。
力の作図ができなくて解けないのか、
運動方程式、作用反作用の法則、摩擦の式・・・方程式が立てられなくて解けないのか、
ただ中学校の範囲の連立方程式を「文字で」できなくて解けないのか。
もう、どこができなくて解けないのか、わかったでしょう?
物理は解説を読んでいるだけでは、解けるようになりません。
物理を解く手順はお見せしました。
物理を解けるようにする具体的な方法もお教えしました。
さあ、次はあなたが手を動かす番です。