問題演習お疲れ様です。
ここからの解答は、
ルールに従って解くこと
を大事にしてます。
どんな問題でも、
確実に解くために。
この目の前の
問題を解けたところで、
入試問題を解けなかったら
意味ないですから。
ルールを身に付ける。
さすれば、
どんな問題でも簡単に解けます。
同じ作業です。
【物理のエッセンス(力学)問91】
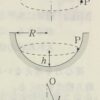
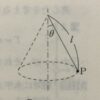
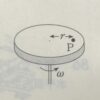
滑らかな水平面上を長さ$l$の糸に結ばれて角速度$ω$で円運動する質量$m$の小球$P$がある。糸の端は高さ$h$の点$o$に固定されている。糸の張力$S$と床からの垂直抗力$N$を求めよ。$ω$がある値$ω_0$をこえると$P$は床から離れる。$ω_0$を求めよ。
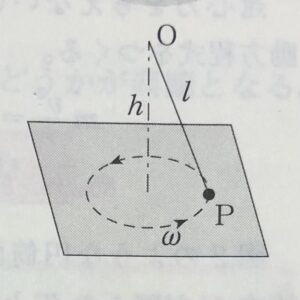
⓪問題文をちゃんと読む。
:与えられた条件、 : 求めるもの。
【物理のエッセンス(力学)問91】
滑らかな水平面上を長さ$l$の糸に結ばれて角速度$ω$で円運動する質量$m$の小球$P$がある。糸の端は高さ$h$の点$o$に固定されている。糸の張力$S$と床からの垂直抗力$N$を求めよ。$ω$がある値$ω_0$をこえると$P$は床から離れる。$ω_0$を求めよ。

①注目する物体を1つに決める。
もちろん、「小球$P$」に決める。
②その物体に働く力を図示する。
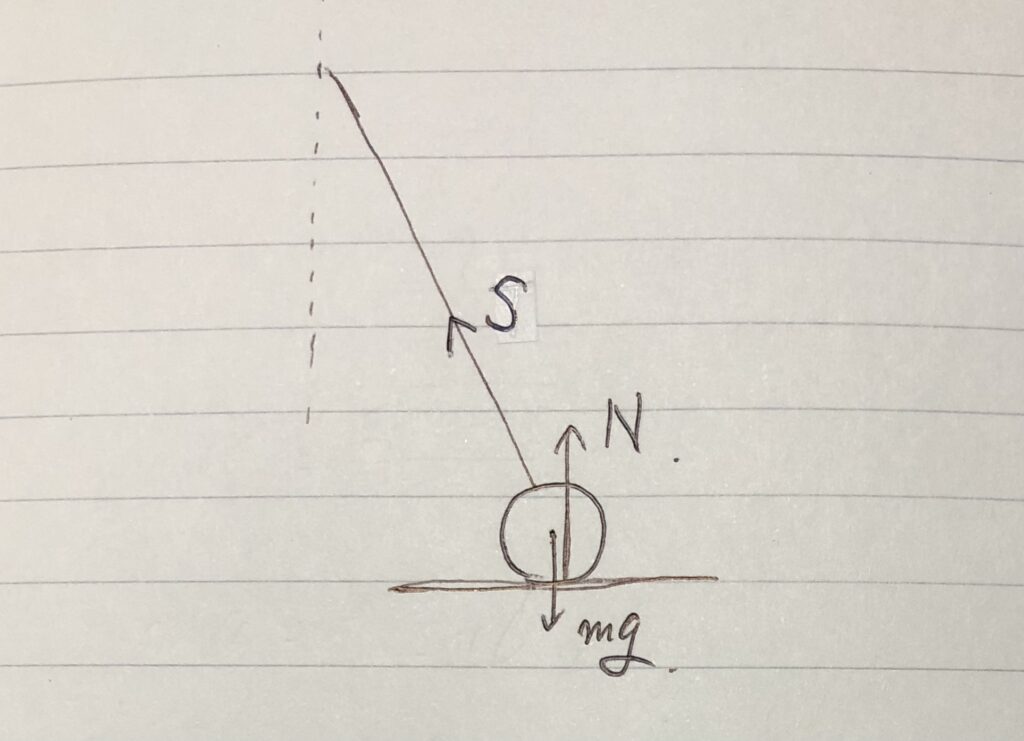
質量$m$をもつ→重力$mg$がかかる。
糸に接する→糸の方向に張力$S$で引っ張られる。
また、
物体同士が接触している。
→必ず、摩擦力と垂直抗力が発生している!
【これが例外なだけ】
床が「なめらか」→摩擦力は0。
壁が「なめらか」→摩擦力は0。
物体の表面は「なめらか」
→摩擦力は0。
小球$P$は床と接しているから、
垂直抗力$N$を書き込む。
(なめらかだから、摩擦力なし)
③$x$軸と$y$軸を設定する。(または$x$軸だけ)
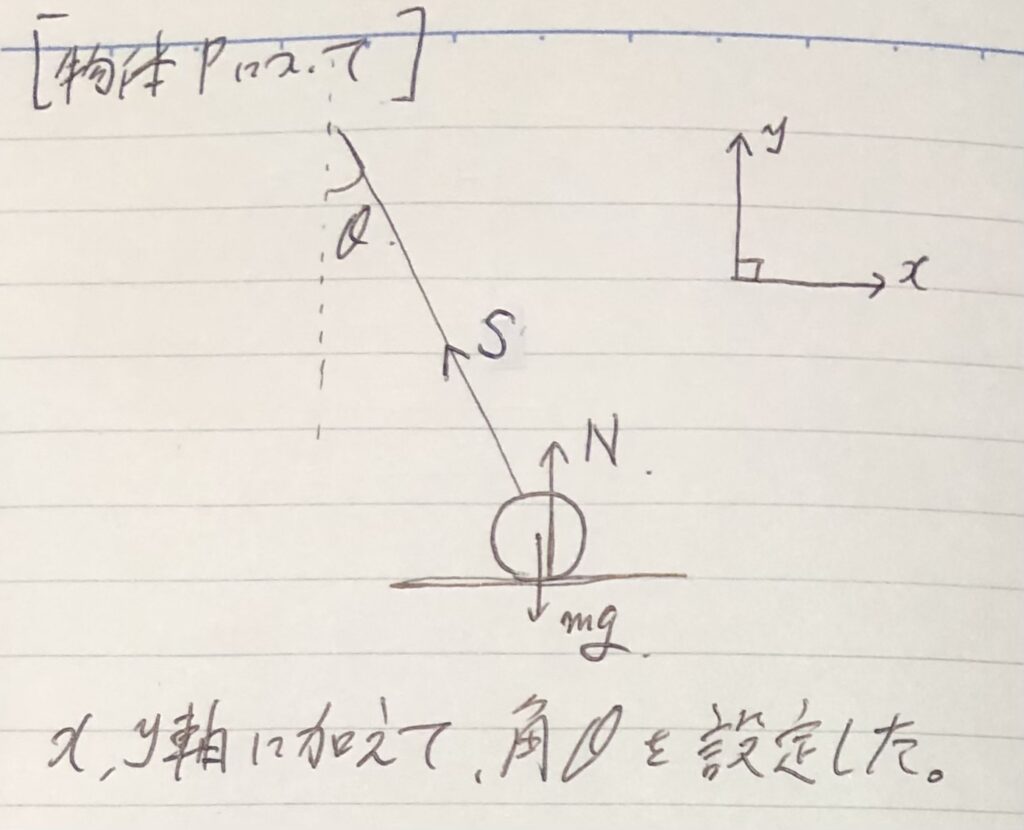
今回は、
物体が3次元で動いているが、
力は2次元(平面)内で発生している。
だから、
立てる軸は$x$軸と$y$軸の
2本でいいんですね。
また、数学的視点から角$θ$を設定した。
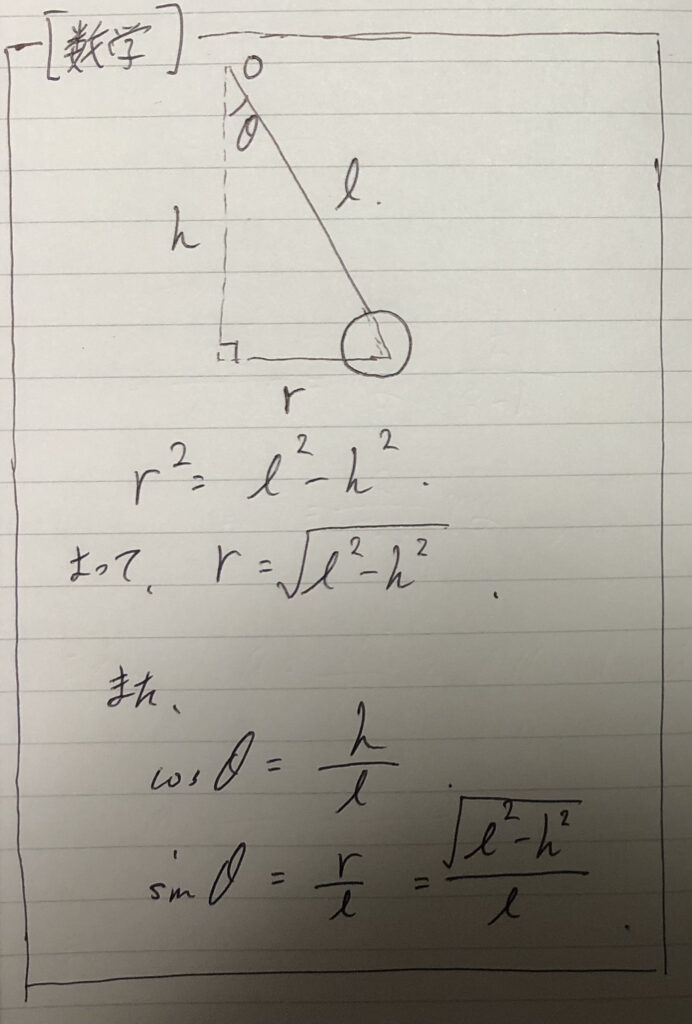
ということですね。
ここは、
数学の話なので・・・
引っかかる場合は
数学(三角関数)を学び直してください。
④力を分解する。
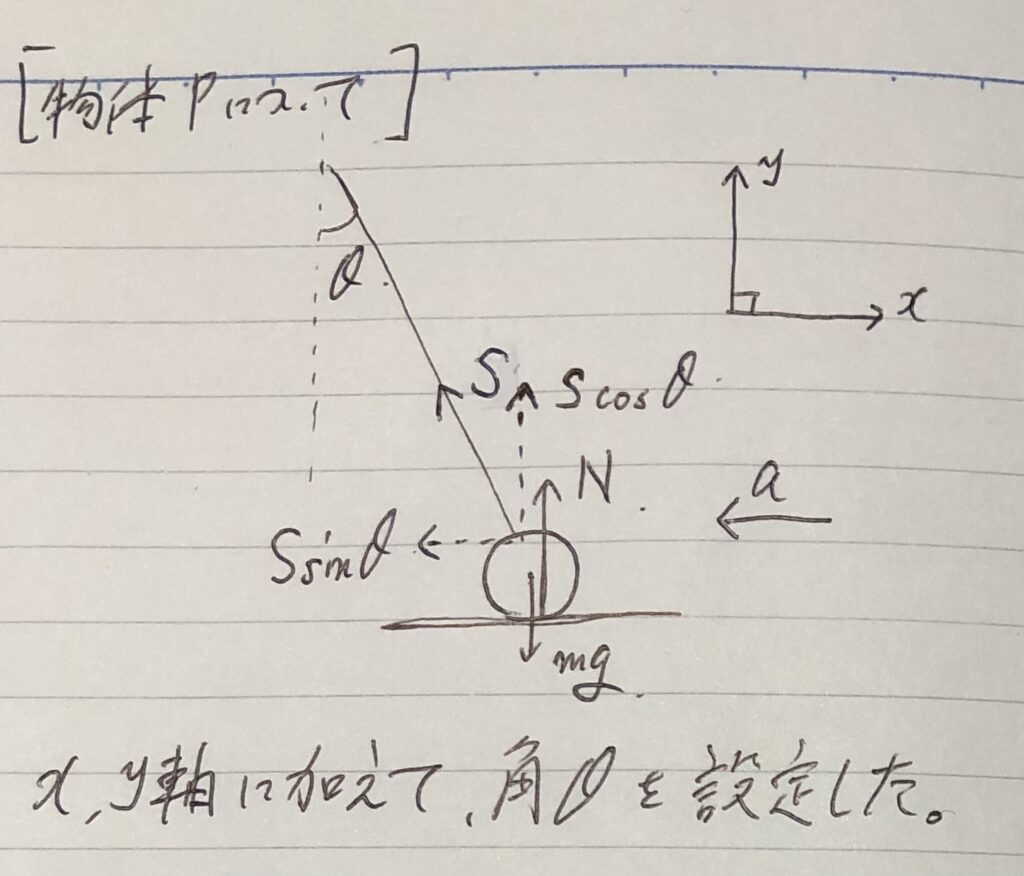
張力$S$を
軸方向に分解しました。
ここも、
わからないなら
数学(幾何学の角度)を学び直してくださいね?
(物理の問題じゃないから)
⑤$x$軸方向と$y$軸方向それぞれで、運動方程式「$ma=F$」に代入する。

加速度$a$は、$x$軸正方向と逆を向いているから、代入するときは「$-a$」で。
ほかの文字も、
正負を間違えないように注意やな。
⑥作用・反作用の法則の等式を立てる。($N=N’$とか、$f=f’$とか。)
今回はなし。
⑨式を計算する。
まずは、ここまでのまとめね。
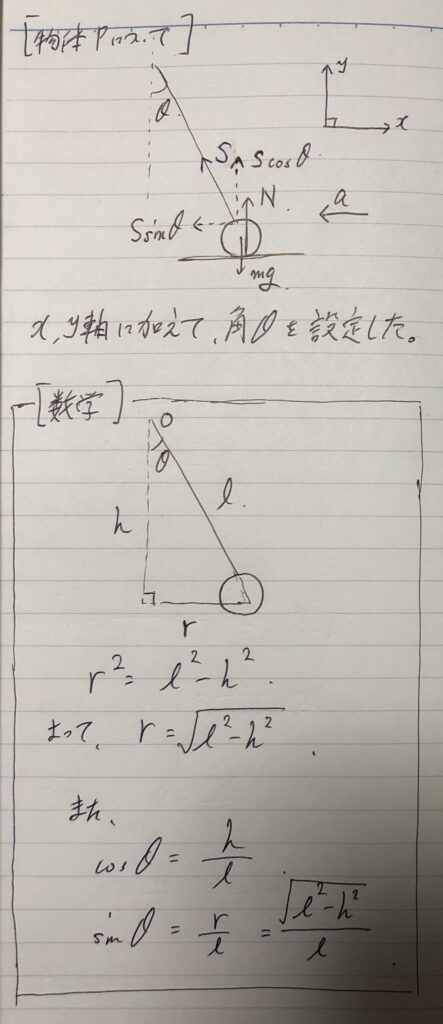

また、
・物体$P$が円運動していること
より、
円の中心方向の加速度が
決定できる。

ということですね。
ここまでが物理。
あとは、数学のお話です。
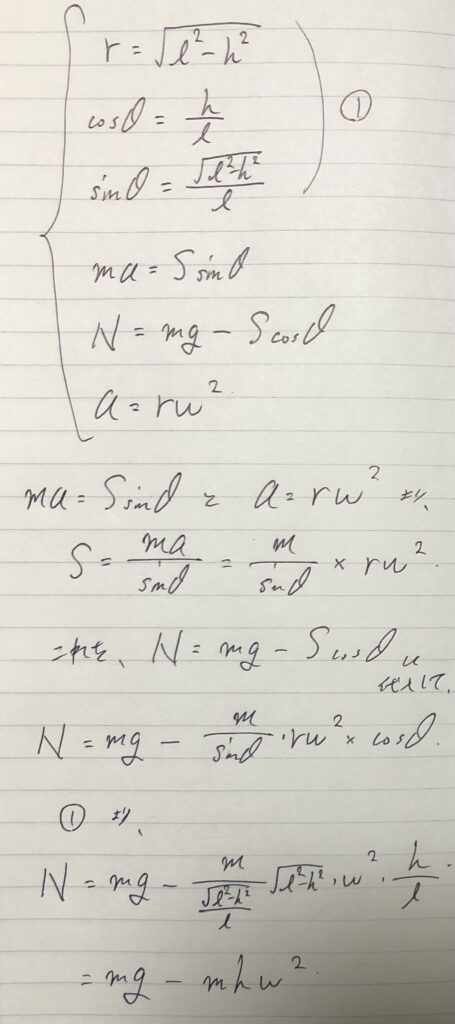

すみません、
$S$を導出してませんでしたね。
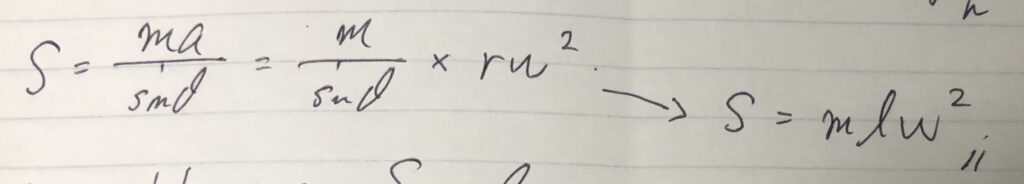
以上です!
これで、
今回の宿題は終わりですね。
お疲れ様でした。