どうも、白滝です。
これでも、家庭教師をやってます。
するとね、、
よく質問がくるんです。
つり合いの式と運動方程式って、
どうやって使い分けるの?
って。
高校生時代、
私もその疑問を持った1人でした。
物体の逆向きに力が働いているから、
つり合いの式を立てたら、、
答えは運動方程式だったとか。
よくありますよね?
つり合いの式って、結局いつ使えばいいの?
運動方程式との使い分けって?
・・・・・・。
ある程度物理をやっていると、
当たり前にぶつかる疑問ですよね。
なぜ、疑問に思うのか?
それ、教科書に書いてないの?
いいえ、、
教科書にはどこにも書いてありません。
少なくとも、
私たちが納得できる書き方では、ね。
つり合いの式と運動方程式を100%使い分ける方法は、めちゃめちゃシンプル。
そう、実はあるのです。
教科書にも、
まあ、、本当は書いてあるのでしょう。
ほら、
習いませんでしたか?
私たちが教えられたのは、
物体に働く力がつり合っていたら、釣り合いの式を立てろ!
って話だったはず。
じゃあ、
いつ「つり合っているのか?」というと、
・物体が動かないというような場合だけでなく、等速度運動しているような場合。
・要するに、複数の力がはたらいているのに物体の運動状態が変化しないような場合、力がつり合っている。
(http://www.wakariyasui.sakura.ne.jp/p/mech/tikara/turiai.htmlより引用)
らしいですよ?
ハハ。
使いもんには、
ならなそうだけれども。
一応、正しいことは書いてあります。
そして、
これがあなたが物理のできない
諸悪の根源です。
知ってました?
あなたが物理をできないのは、
教科書があまりに悲惨だからです。
やる気がない。
教える気がない。
つり合いの式と運動方程式の違いって?どうやって使い分けるの?
って疑問も、
物理の教科書が
ちゃんと教えないから悪いんです。
本当はね、
めちゃシンプルなのに。
ごちゃごちゃと日本語を並べたがる。
では、
ここからはシンプルにいきましょう。
物理は、物理らしく。
物体の加速度が0→つり合いの式も使えるよーんっ
はい。
これが、
つり合いの式と運動方程式の使い分け、
です。
「物体の加速度が0→つり合いの式も使えるよーんっ」の解説をしちゃうぞ
「物体に働く力がつり合っている」とは何か?
→物体の加速度が0だってことです。
こんだけ。
つり合いの式が使える条件。
なぜ、教科書はあんなに日本語を並べたがるのでしょう?
物体の加速度が0→つり合いの式が使える
で100点じゃないですか。
加速度があるかどうか。
だってね、
運動方程式(F=ma)の加速度aに0を代入したのが、
つり合いの式ですから。
わかります?
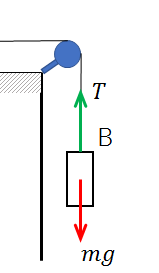
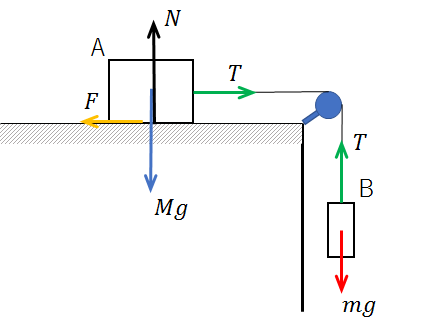
仮に、
この物体Bが
加速度αで上に上がっていったとしたら、
F=mα → T-mg=mα
が成り立ちますよね?
これが、運動方程式。
でも、ここでね、
もし仮に加速度α=0だったとすると、
F=mα → T-mg=m×0
→T-mg=0
→T=mg
って、
運動方程式が
つり合いの式になるんですよねー
わかります?
運動方程式F=mαって、
(正の方向の力)ー(負の方向の力)=mα
だからね?(公式)
加速度が0(αが0)の時は、
(正の方向の力)ー(負の方向の力)=m×0
→(正の方向の力)ー(負の方向の力)=0
→(正の方向の力)=(負の方向の力)
ってなるの。
おわかり?
つまりはね、
つり合いの式って運動方程式の「加速度が0」バージョン
ってことなんだな。
知ってた?
知ってたら、
つり合いの式と運動方程式の違いって?どうやって使い分けるの?
とかバカなことで悩まない。
だって、
加速度がどうであれ、
いつも運動方程式だけで解けるんだから。
つり合いの式なんて使わずに、
運動方程式を立てて、たまたま加速度が0なら、
つり合いの式みたいに解けばいいじゃん。
要は、加速度なんです。
もっと実用的に書くと、
・物体に働く加速度が0→つり合いの式が立てれる。
・物体に働く加速度が「0かどうか分からない」→運動方程式。
を使えばOK。
ここ、メモるとこですよ?
まず、物体に働く加速度
に着目する。
物体の加速度がゼロだと確認できる
→つり合いの式を立てる。
加速度が0かどうか、わからない
→運動方程式を立てる。
ですからね?
たとえ運動方程式を立てた後に、
物体の加速度が0だとわかっても、
解けますから。
つり合いの式は
運動方程式の「加速度0」バージョン
だからです。
ね?
裏技でもなんでもなく、これが物理の真理。
シンプルな物理学を、
ごちゃごちゃ複雑にした教科書が悪い。
私たちは、
今日もシンプルに学んでいきましょう!
へへ。
それでは!