問題演習お疲れ様です。
ここからの解答は、
ルールに従って解くこと
を大事にしてます。
どんな問題でも、
確実に解くために。
この目の前の
問題を解けたところで、
入試問題を解けなかったら
意味ないですから。
ルールを身に付ける。
さすれば、
どんな問題でも簡単に解けます。
同じ作業です。
【物理のエッセンス(力学)問46】
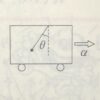
質量$M$の$A$に質量$m$、長さ$l$のロープを取り付け、なめらかな床上を$F$の力で引っぱる。付け根から$x$離れた位置でのロープの張力$T$を求めよ。
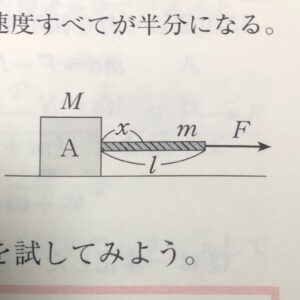
⓪問題文をちゃんと読む。
:与えられた条件、 : 求めるもの。
【物理のエッセンス(力学)問46】
質量$M$の$A$に質量$m$、長さ$l$のロープを取り付け、なめらかな床上を$F$の力で引っぱる。付け根から$x$離れた位置でのロープの張力$T$を求めよ。

この問題は「ロープ」「張力$T$」とか言っているが、
質量のある「糸(ロープ)」は糸じゃない。物体だ。
そう。
質量があるなら、物体なのである。
だから、
通常の糸、張力の考え方は使えないのだ。
だから「物体のなか」の位置$x$
での張力が欲しければ、
位置$x$で物体を分割して考えるしかない。
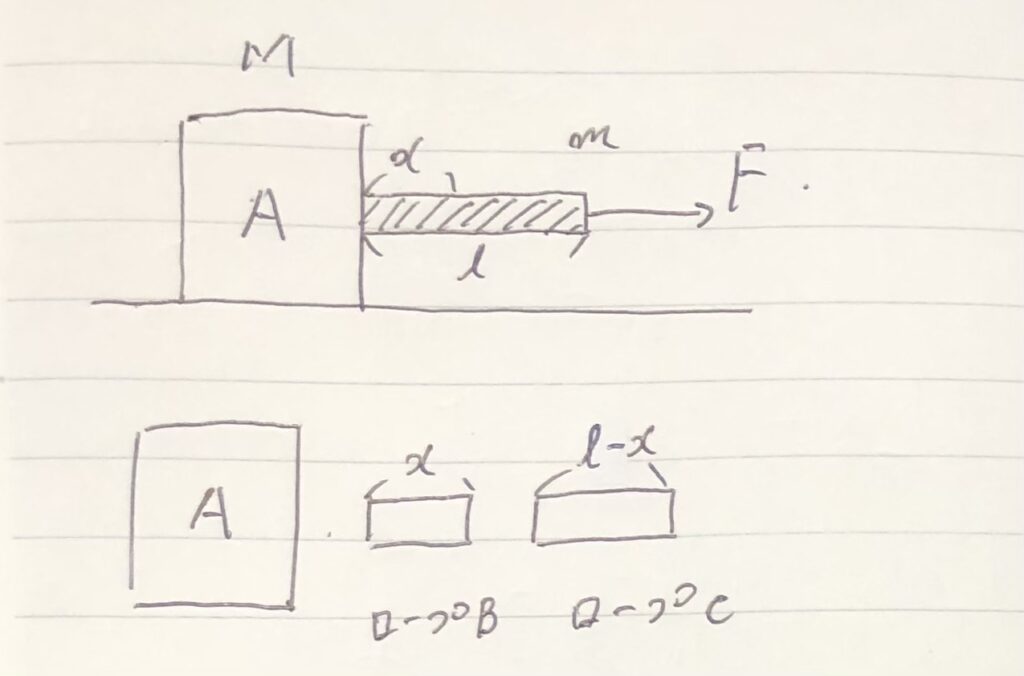
今回は
ロープを2つに分解。
それらを「ロープ$B$」「ロープ$C$」とおく。
それらの質量は、
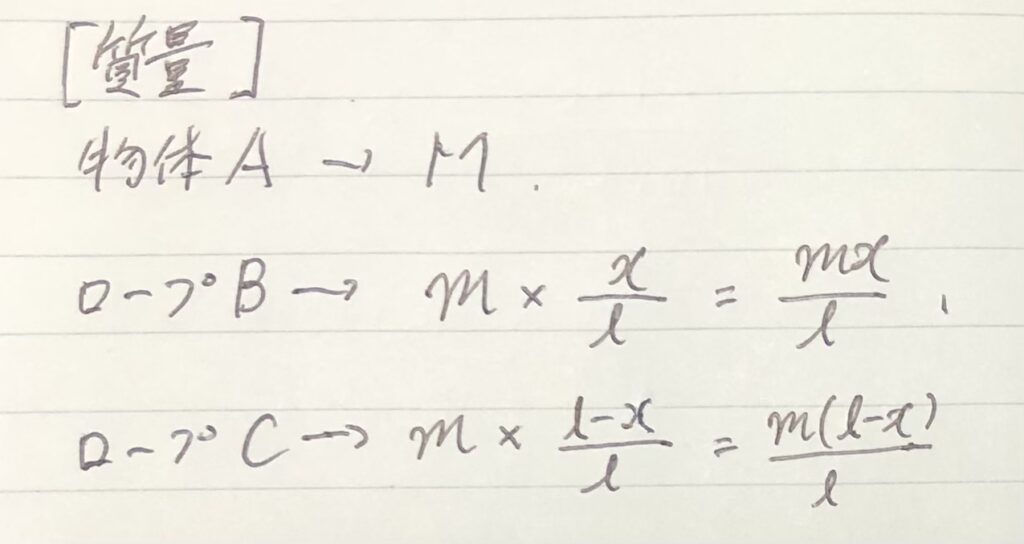
と計算できる。(ここは数学)
①注目する物体を1つに決める。
とりあえず「物体$A$」に決める。
②その物体に働く力を図示する。
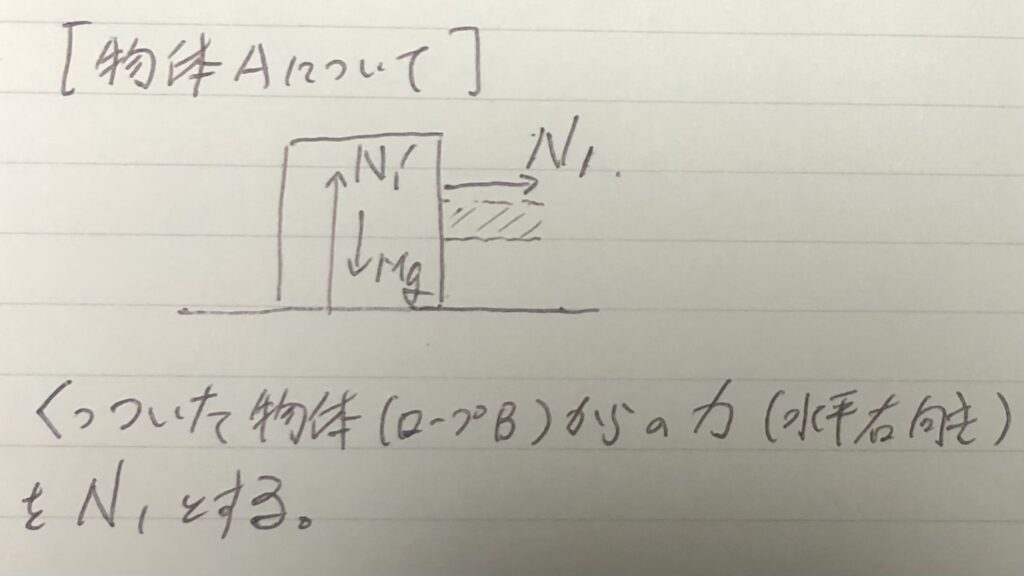
質量$M$をもつ→重力$Mg$がかかる。
ロープ$B$とくっ付く→物体(ロープ$B$)の方向に、力$N_1$で引っ張られる。
(もちろん鉛直方向に「ロープ$B$との摩擦力」も発生しますが、忘れてましたw今回は$y$軸方向で式を立てないので大丈夫です)
→必ず、垂直抗力(くっ付いている場合は張力)と摩擦力が発生する。
ですから。忘れずに。
③$x$軸と$y$軸を設定する。(または$x$軸だけ)
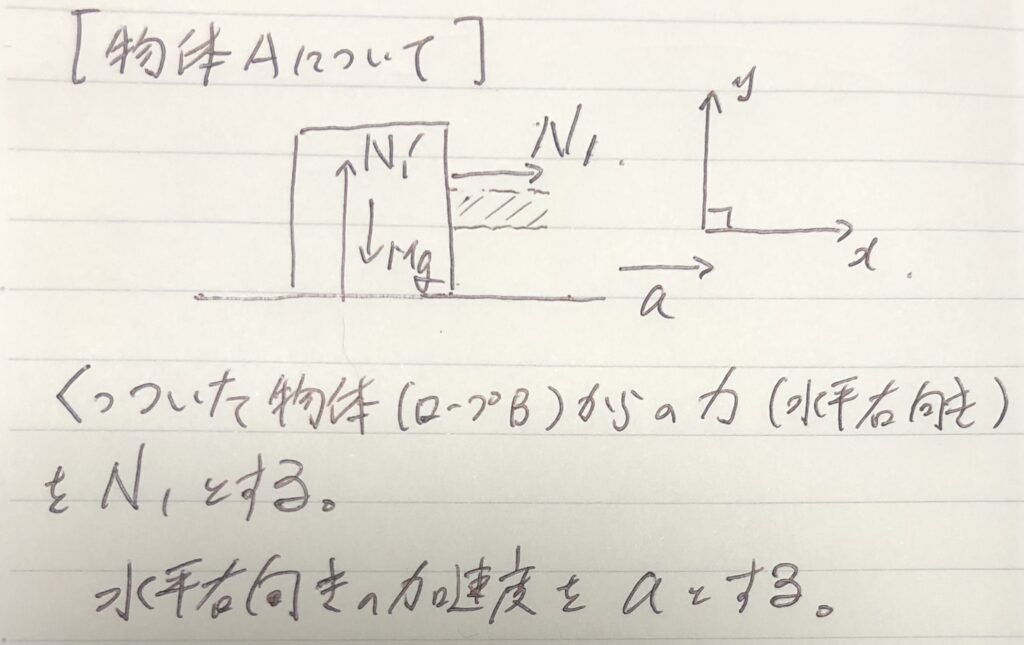
④力を分解する。
今回はなし。
⑤$x$軸方向と$y$軸方向それぞれで、運動方程式「$ma=F$」に代入する。
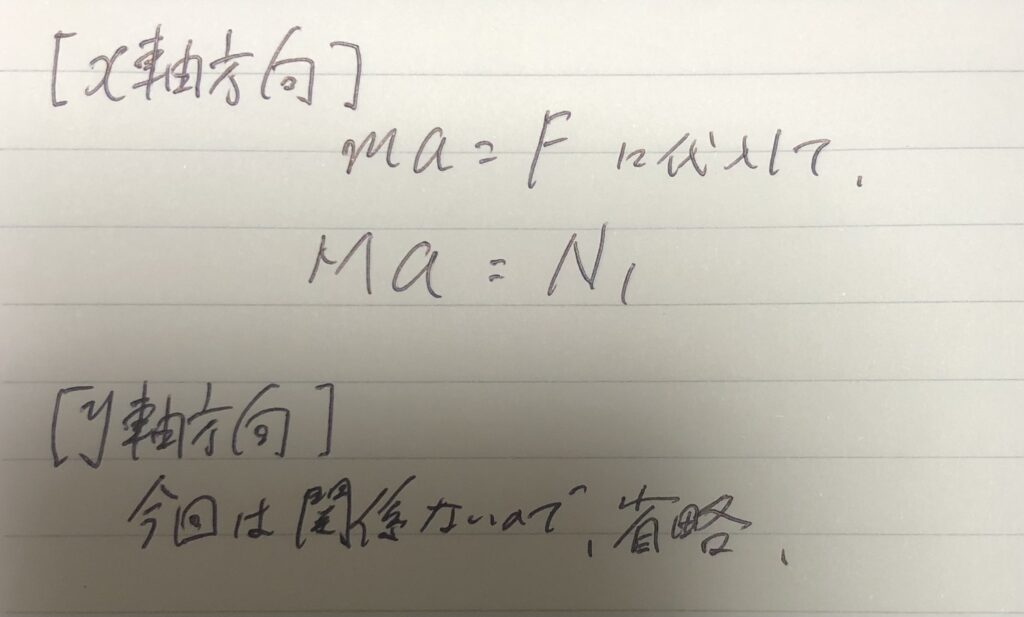
⑥別の、注目する物体を1つに決める。(2つ目)
「ロープ$B$」に決める。
⑦力を図示して、軸を設定して、力を分解する。

【水平方向($x$軸)だけ考える】
質量$\frac{mx}{l}$をもつ→重力$\frac{mx}{l}g$がかかる、が鉛直方向なので考えない。
また、
→必ず、垂直抗力(くっ付いている場合は張力)と摩擦力が発生する。
よって、
物体$A$とくっ付く→物体$A$の方向に、張力$N_1$で引っ張られる。
ロープ$C$とくっ付く→ロープ$C$の方向に、張力$N_2$で引っ張られる。
(摩擦力は存在するが、鉛直方向なので考えない)
→そして、公式に代入する。
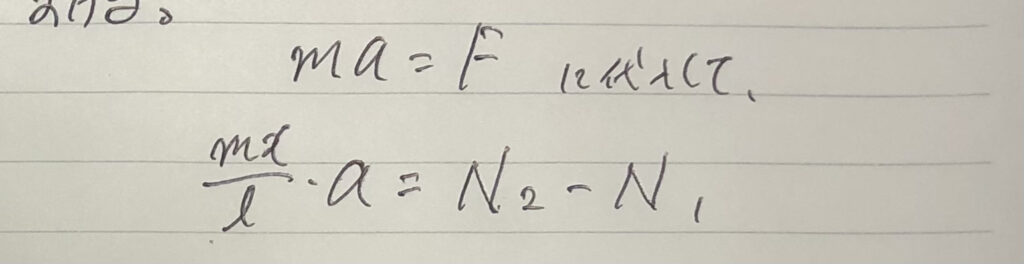
⑥-2別の、注目する物体を1つに決める。(3つ目)
「ロープ$C$」に決める。
⑦-2力を図示して、軸を設定して、力を分解する。

【水平方向($x$軸)だけ考える】
質量$\frac{m(l-x)}{l}$をもつ→重力$\frac{m(l-x)}{l}g$がかかる、が鉛直方向なので考えない。
問題文から→力$F$を水平右向きに受ける。
また、
→必ず、垂直抗力(くっ付いている場合は張力)と摩擦力が発生する。
よって、
ロープ$B$とくっ付く→ロープ$B$の方向に、張力$N_2$で引っ張られる。
(摩擦力は存在するが、鉛直方向なので考えない)
→そして、公式に代入する。
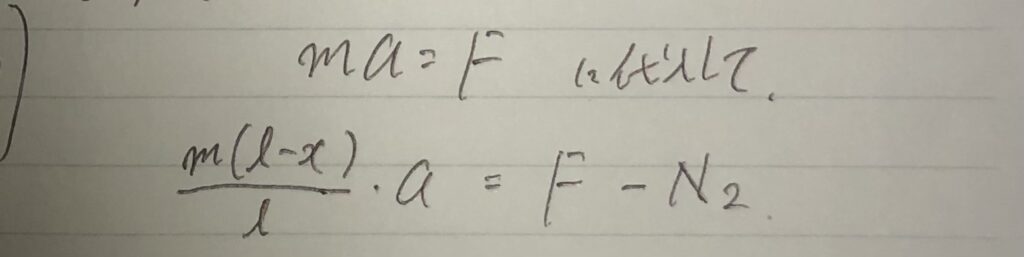
⑧作用・反作用の法則の等式を立てる。($N=N’$とか、$f=f’$とか。)
今回はなし。
⑨式を計算する。
これは、今までのまとめ。


ここまでは物理。
あとは、数学のハナシ。
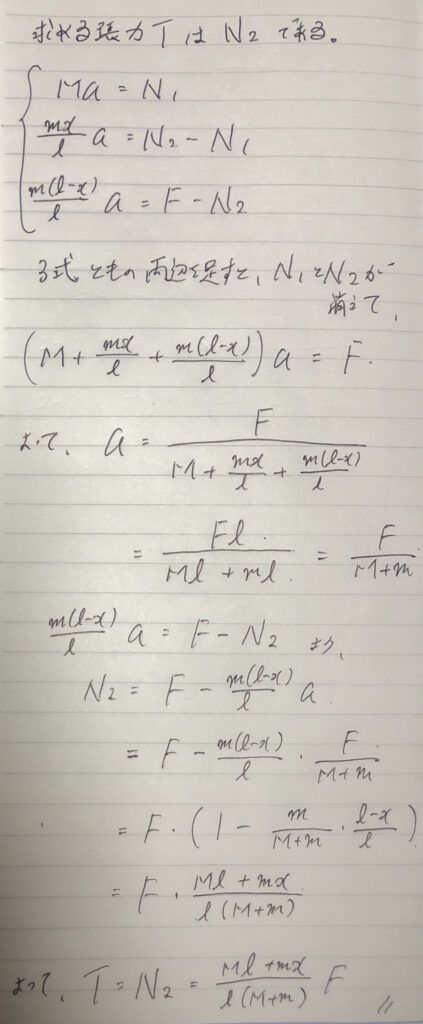
以上です!
次は
問題47ですね。
お疲れ様でした。