目次
張力、垂直抗力、バネの「力の作図」はみな同じ。
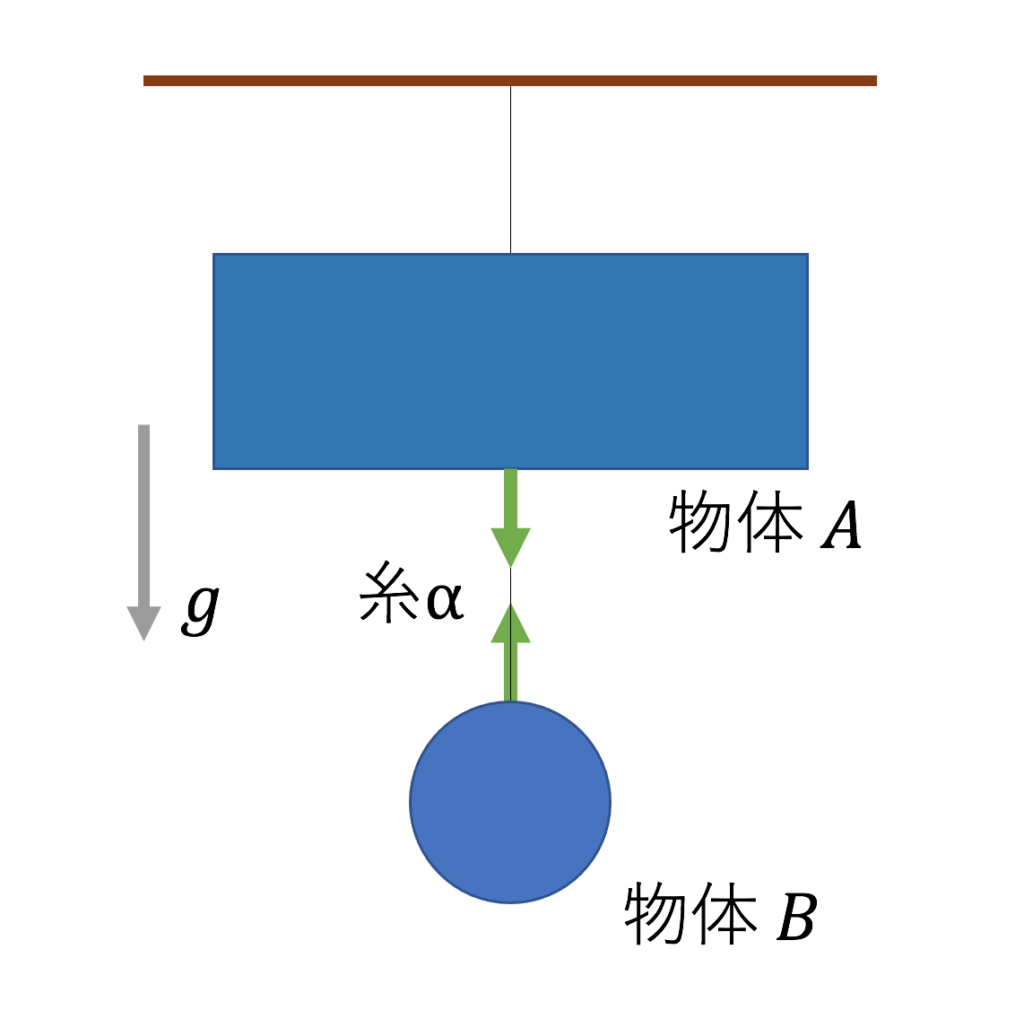
張力=垂直抗力=バネの力。
どれも、
というだけ。
「力の作図」でやることは、全部同じなのだ。
ただ、矢印を書けばいい。
また、
同じ糸、バネから受ける力は常に等しい。
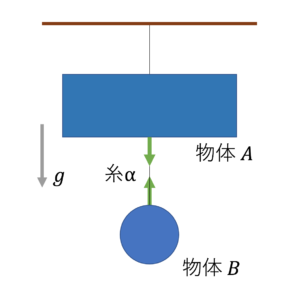
同じ糸から受ける力は、すべて等しい。
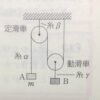
物体$A$が糸$α$から受ける力:$T$
物体$B$が糸$α$から受ける力:$T$
同様に、
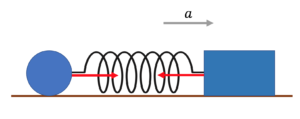
同じバネから受ける力は、すべて等しい。
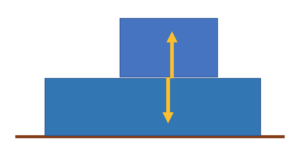
垂直抗力は互いに等しい。
これらはすべて、作用・反作用の法則による。
(糸とバネにも適用されるのは、糸とバネの質量が$0$だから)
つまり、
垂直抗力→互いの物体にはたらく力は同じ$N$
バネの力→両端の物体にはたらく力は同じ$F$
となるわけだ。
はたらく力が必ず、
作用・反作用の関係になる。
2つの物体に
はたらく力の大きさが、同じになる。
じゃあ、バネって?
バネって何が違ったのだろうか?
バネとは、計算時に違いを発揮するのだ。
【バネだけ+α】
計算するときに、
「$F=kx$」と「$U=\frac{1}{2}kx^2$」
が使える。
ただそれだけ。
バネだけ、計算時に違いがある。
・自然長からの伸び$x$で、$F$が計算できる。
・位置エネルギー$U=\frac{1}{2}kx^2$をもつ。
これは、
張力と垂直抗力にはない特性。
でも、それだけなのだ。
張力と垂直抗力、バネの違いって。
知ってましたか?
それ以外は、
張力=垂直抗力=バネの力
だと思っていればいい。
(もちろん、扱い方のハナシ)
たとえばね・・・
力の作図をするときは、
バネのあのぐるんぐるんは「ピンと張った1本の糸」だと思って、
力$F$を書き込んでやれば良いのだ。
たとえば、この図は
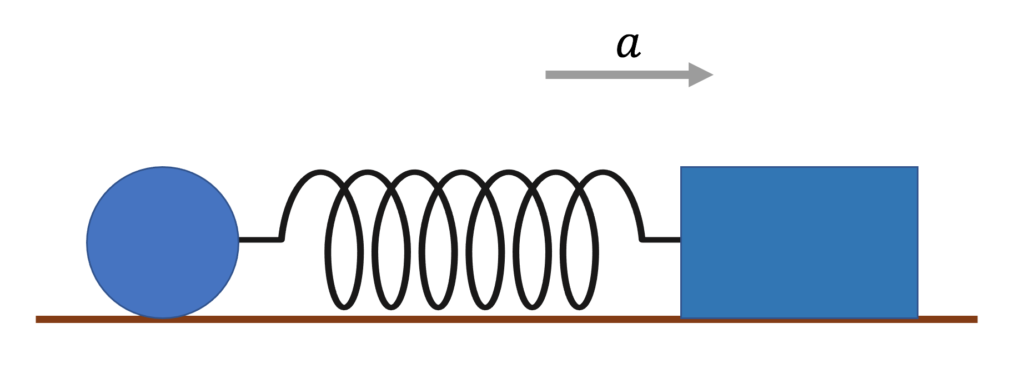
バネを糸に書き換えて(そうみなして)
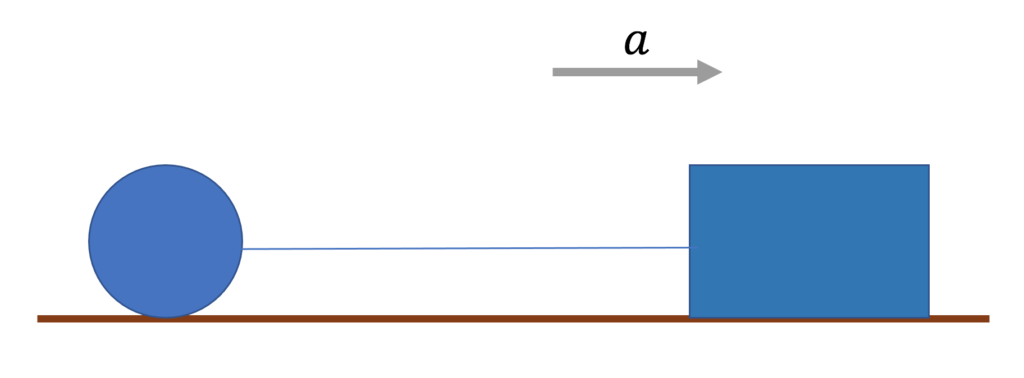
力$F$を作図してやって、
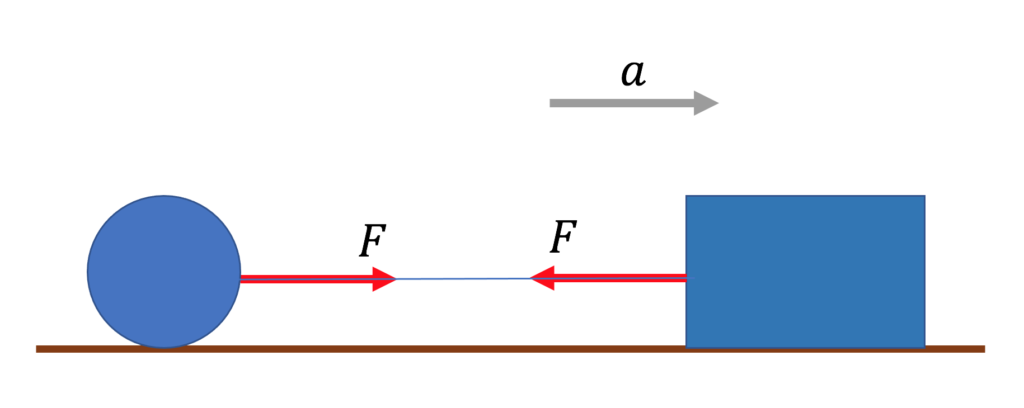
元に戻すと、こうなっている。
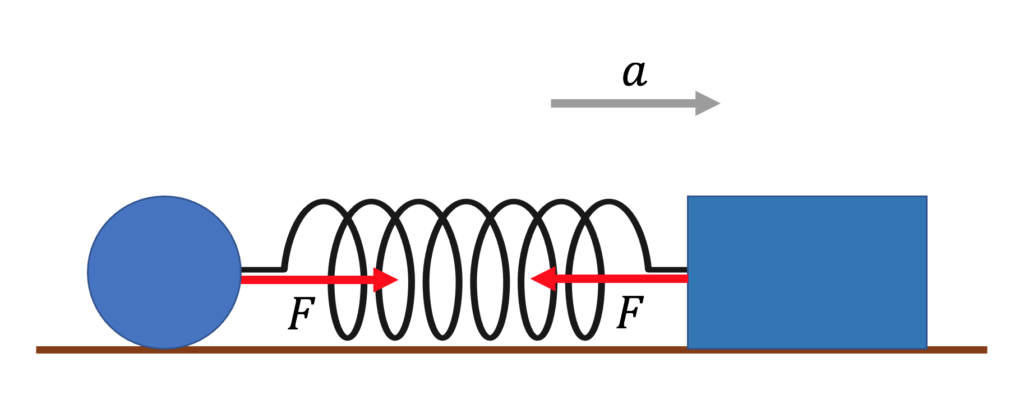
まあ、
バネと糸の扱いは同じなのだから、
頭の中で糸に変換してあげると
スムーズに解けたりするんだね。
とくに、力の作図。
基本的に、
バネは糸と同じ扱いなのだから。
違うのは、
計算するときだけ。
あとは、
張力が$0$になったときに
(くっ付いた)バネ→ゆるまない。
糸→糸がゆるんで、力が発生しなくなる。
ってだけかな。
まあ、
バネと糸は非常に似ている
ってことが頭にあると、力の作図がしやすくなる。
張力と垂直抗力、バネの全パターンって?
よく見るパターンはこんな感じだね。
【糸の張力】
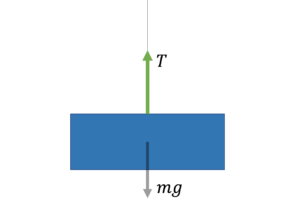
$T=0$になったら、糸がゆるむ。
【(くっ付かない物体との)垂直抗力】
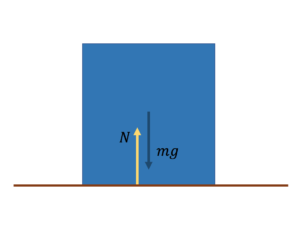
$N=0$になったら、離れる。
【「くっ付いた」バネ】
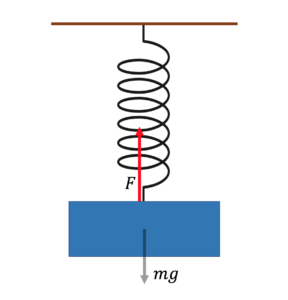
$F>0$→引っ張る力(張力)
$F<0$→押す力(垂直抗力)
そして、
【糸の張力】
$T=0$になったら、糸がゆるむ。
【(くっ付かない物体との)垂直抗力】
$N=0$になったら、離れる。
【「くっ付いた」バネ】
$F>0$→引っ張る力(張力)
$F<0$→押す力(垂直抗力)
という条件はよく使われる。
要はね、
(接続しているのか、してないのか)
で、条件が変わってくるのだ。
だから、難易度が上がると・・・
【くっ付いた物体との張力】
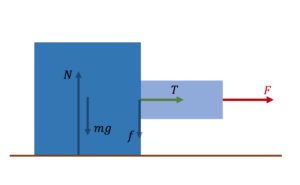
$T$がマイナスになったら、垂直抗力(逆向き)に変わる。
【くっ付いた物体との垂直抗力】

$N_2$がマイナスになったら、張力(逆向き)に変わる。
【「くっ付いていない」バネ】
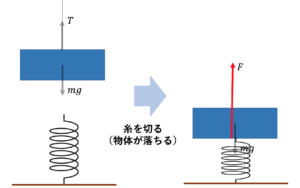
$F=0$になったら、物体が離れる。
とくに最後の「くっ付いていない」バネは、
条件がわからずに失敗してしまう受験生が多い。
また、
くっ付いていると、
他の力次第で
張力が垂直抗力に逆転したり。
【糸の張力】
$T=0$になったら、糸がゆるむ。
【(くっ付かない物体との)垂直抗力】
$N=0$になったら、離れる。
は有名で重要だが、
それ以外にもパターンがあるのだ。
張力と垂直抗力とバネ。
大事な視点として、
「くっ付いているかどうか?」
をみて欲しい。
この6パターンがすべて
なので。
これが無意識に扱えれば、
張力と垂直抗力、バネは免許皆伝ですよ。
まったくの敵なしです。
ご参考までに。